MPZI_predavanje_08 -- Sage

(Za „lijepi” ispis svih rezultata označite kvadratić kraj riječi Typeset.)

Elementi matematičke analize (2)

Integrali

Određeni integrali

Geometrijski, vrijednost određenoga integrala funkcije $\boldsymbol{f}$ jedne varijable u granicama od $\boldsymbol{a}$ do $\boldsymbol{b}$ , $A = \displaystyle\int_a^b f(x)\,dx$ , uz $a < b$ , jednaka je „ploštini” površine između krivulje kojom je funkcija $f$ predočena (grafa funkcije $f$ ), osi $x$ i ordinala u točkama $a$ i $b$ :

f(x) = sin(x) + 1/2*sin(5*x)
a = 0.325
b = 2.425

pf = plot (f, (x, 0, pi), thickness = 0.5)
parea = plot (f, (x, a, b), thickness = 1.5, fill = True,)
oa = line ([(a, 0.), (a, f(a))], thickness = 1.5, color = 'green')
ob = line ([(b, 0.), (b, f(b))], thickness = 1.5, color = 'green')
px = line ([(a, 0.), (b, 0)], thickness = 2, color = 'magenta')
(pf + parea + oa + ob + px).show (figsize = 6)

area = integral (f, x, a, b)
area

$\newcommand{\Bold}[1]{\mathbf{#1}}1.6058644239859046$

Ako je graf funkcije ispod osi $x$ (to jest, ako su vrijednosti funkcije negativne), dobivena je „ploština” negativna:

pf = plot (f, (x, -pi, 0), thickness = 0.5)
parea = plot (f, (x, -b, -a), thickness = 1.5, fill = True)
oa = line ([(-a, 0.), (-a, f(-a))], thickness = 1.5, color = 'green')
ob = line ([(-b, 0.), (-b, f(-b))], thickness = 1.5, color = 'green')
px = line ([(-b, 0.), (-a, 0)], thickness = 2, color = 'magenta')
(pf + parea + oa + ob + px).show (figsize = 6)

integral (f, x, -b, -a)

$\newcommand{\Bold}[1]{\mathbf{#1}}-1.6058644239859046$

... tako da je, primjerice,

integral (f, x, -pi, pi)

$\newcommand{\Bold}[1]{\mathbf{#1}}0$

pf = plot (f, (x, -pi-0.2, pi+0.2), thickness = 0.5, figsize = 6)
parea = plot (f, (x, -pi, pi), thickness = 1.5, fill = True, figsize = 6)
px = line ([(-pi, 0.), (pi, 0)], thickness = 2, color = 'magenta')
pf + parea + px

... i još jedan primjer:

integral (sin(2*x) * sin(x/4), x, 0, 4*pi)

$\newcommand{\Bold}[1]{\mathbf{#1}}0$

plot (sin(2*x) * sin(x/4), (x, 0, 4*pi), fill = True, figsize = 6)

Zamijene li se granice integracije, vrijednost integrala mijenja predznak:

integral (f, x, a, b); integral (f, x, b, a)

$\newcommand{\Bold}[1]{\mathbf{#1}}1.6058644239859046$

$\newcommand{\Bold}[1]{\mathbf{#1}}-1.6058644239859046$

integral (f, x, -a, -b); integral (f, x, -b, -a)

$\newcommand{\Bold}[1]{\mathbf{#1}}1.6058644239859046$

$\newcommand{\Bold}[1]{\mathbf{#1}}-1.6058644239859046$

I, naravno:

integral (f, x, a, a)

$\newcommand{\Bold}[1]{\mathbf{#1}}0$

Nazivi funkcija integral() i integrate() su sinonimi, a još su neki oblici poziva:

integral (f, (x, a, b))

$\newcommand{\Bold}[1]{\mathbf{#1}}1.6058644239859046$

integral (f(x), (x, a, b))

$\newcommand{\Bold}[1]{\mathbf{#1}}1.6058644239859046$

integrate (f, x, a, b)

$\newcommand{\Bold}[1]{\mathbf{#1}}1.6058644239859046$

integrate (f, (x, a, b))

$\newcommand{\Bold}[1]{\mathbf{#1}}1.6058644239859046$

f.integral (x, a, b)

$\newcommand{\Bold}[1]{\mathbf{#1}}1.6058644239859046$

f(x).integral (x, a, b)

$\newcommand{\Bold}[1]{\mathbf{#1}}1.6058644239859046$

Jedna primjena u mehanici

Sila $\vec{F}$ djeluje na pravcu osi $x$ , $\vec{F} = F\,\vec{\imath}$ , a njezina je vrijednost $F$ funkcija položaja njezina hvatišta, $F : x \mapsto F(x)$ . Ako se njezino hvatište pomakne od točke $x_0$ do točke $x_1$ , mehanički je rad sile $\vec{F}$ na tom pomaku

$W \,=\, \displaystyle\int_{x_0}^{x_1} F(x)\, dx$ .

F(x) = -2/x^2
x0 = 2
x1 = 1 
W = integral (F, x, x0, x1)
W

$\newcommand{\Bold}[1]{\mathbf{#1}}1$

p1 = plot (F(x), (x, 0.4, 2.2), ymax = 5, figsize = 6)
p2 = plot (F(x), (x, 1, 2), fill = True, figsize = 6)
p1 + p2

Kako je $F<0$ , sila i pomak od točke $x_0 = 2$ do točke $x_1 = 1$ jednako su orijentirani, pa je rad pozitivan. Ako je pak sila orijentirana suprotno od pomaka (primjerice, ako je pomak od $x_1 = 1$ do $x_0 = 2$ ), rad je negativan (kažemo da se sila odupire pomaku):

integral (F, x, x1, x0)

$\newcommand{\Bold}[1]{\mathbf{#1}}-1$

Ako nema pomaka, rad je jednak nuli:

integral (F, x, x0, x0)

$\newcommand{\Bold}[1]{\mathbf{#1}}0$

Beskonačnosti dohvatljive i nedohvatljive

log (0)

$\newcommand{\Bold}[1]{\mathbf{#1}}-\infty$

plot (log(x), (x, 0, 1), ymin = -10, fill = True, figsize = 6)

... ali:

integral (log(x), (x, 0, 1))

$\newcommand{\Bold}[1]{\mathbf{#1}}-1$

Međutim,

plot (-1/x, (x, 0, 1), ymin = -100, fill = True, figsize = 6)

integral (-1/x, (x, 0, 1))

Traceback (click to the left of this block for traceback)
...
ValueError: Integral is divergent.

Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
  File "_sage_input_59.py", line 10, in <module>
    exec compile(u'open("___code___.py","w").write("# -*- coding: utf-8 -*-\\n" + _support_.preparse_worksheet_cell(base64.b64decode("aW50ZWdyYWwgKC0xL3gsICh4LCAwLCAxKSk="),globals())+"\\n"); execfile(os.path.abspath("___code___.py"))
  File "", line 1, in <module>
    
  File "/tmp/tmpoPtex9/___code___.py", line 3, in <module>
    exec compile(u'integral (-_sage_const_1 /x, (x, _sage_const_0 , _sage_const_1 ))
  File "", line 1, in <module>
    
  File "/opt/SageMath/local/lib/python2.7/site-packages/sage/misc/functional.py", line 753, in integral
    return x.integral(*args, **kwds)
  File "sage/symbolic/expression.pyx", line 12366, in sage.symbolic.expression.Expression.integral (build/cythonized/sage/symbolic/expression.cpp:69760)
  File "/opt/SageMath/local/lib/python2.7/site-packages/sage/symbolic/integration/integral.py", line 820, in integrate
    return definite_integral(expression, v, a, b, hold=hold)
  File "sage/symbolic/function.pyx", line 998, in sage.symbolic.function.BuiltinFunction.__call__ (build/cythonized/sage/symbolic/function.cpp:11922)
  File "sage/symbolic/function.pyx", line 487, in sage.symbolic.function.Function.__call__ (build/cythonized/sage/symbolic/function.cpp:6848)
  File "sage/symbolic/function.pyx", line 1086, in sage.symbolic.function.BuiltinFunction._evalf_or_eval_ (build/cythonized/sage/symbolic/function.cpp:13207)
  File "/opt/SageMath/local/lib/python2.7/site-packages/sage/symbolic/integration/integral.py", line 180, in _eval_
    return integrator(*args)
  File "/opt/SageMath/local/lib/python2.7/site-packages/sage/symbolic/integration/external.py", line 34, in maxima_integrator
    result = maxima.sr_integral(expression, v, a, b)
  File "/opt/SageMath/local/lib/python2.7/site-packages/sage/interfaces/maxima_lib.py", line 811, in sr_integral
    raise ValueError("Integral is divergent.")
ValueError: Integral is divergent.

integral (-1/x, (x, 1e-170, 1))

$\newcommand{\Bold}[1]{\mathbf{#1}}-391.4394658089878$

integral (-1/x, (x, 1, oo))

Traceback (click to the left of this block for traceback)
...
ValueError: Integral is divergent.

Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
  File "_sage_input_61.py", line 10, in <module>
    exec compile(u'open("___code___.py","w").write("# -*- coding: utf-8 -*-\\n" + _support_.preparse_worksheet_cell(base64.b64decode("aW50ZWdyYWwgKC0xL3gsICh4LCAxLCBvbykp"),globals())+"\\n"); execfile(os.path.abspath("___code___.py"))
  File "", line 1, in <module>
    
  File "/tmp/tmpncHEjP/___code___.py", line 3, in <module>
    exec compile(u'integral (-_sage_const_1 /x, (x, _sage_const_1 , oo))
  File "", line 1, in <module>
    
  File "/opt/SageMath/local/lib/python2.7/site-packages/sage/misc/functional.py", line 753, in integral
    return x.integral(*args, **kwds)
  File "sage/symbolic/expression.pyx", line 12366, in sage.symbolic.expression.Expression.integral (build/cythonized/sage/symbolic/expression.cpp:69760)
  File "/opt/SageMath/local/lib/python2.7/site-packages/sage/symbolic/integration/integral.py", line 820, in integrate
    return definite_integral(expression, v, a, b, hold=hold)
  File "sage/symbolic/function.pyx", line 998, in sage.symbolic.function.BuiltinFunction.__call__ (build/cythonized/sage/symbolic/function.cpp:11922)
  File "sage/symbolic/function.pyx", line 487, in sage.symbolic.function.Function.__call__ (build/cythonized/sage/symbolic/function.cpp:6848)
  File "sage/symbolic/function.pyx", line 1086, in sage.symbolic.function.BuiltinFunction._evalf_or_eval_ (build/cythonized/sage/symbolic/function.cpp:13207)
  File "/opt/SageMath/local/lib/python2.7/site-packages/sage/symbolic/integration/integral.py", line 180, in _eval_
    return integrator(*args)
  File "/opt/SageMath/local/lib/python2.7/site-packages/sage/symbolic/integration/external.py", line 34, in maxima_integrator
    result = maxima.sr_integral(expression, v, a, b)
  File "/opt/SageMath/local/lib/python2.7/site-packages/sage/interfaces/maxima_lib.py", line 811, in sr_integral
    raise ValueError("Integral is divergent.")
ValueError: Integral is divergent.

plot (-1/x, (x, 1, 100), fill = True, figsize = 6)

integral (-1/x, (x, 1, 1e170))

$\newcommand{\Bold}[1]{\mathbf{#1}}-391.4394658089878$

plot (-1/x^2, (x, 1, 10), fill = True, figsize = 6)

integral (-1/x^2, (x, 1, oo))

$\newcommand{\Bold}[1]{\mathbf{#1}}-1$

integral (-1/x^2, (x, 0, 1))

Traceback (click to the left of this block for traceback)
...
ValueError: Integral is divergent.

Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
  File "_sage_input_66.py", line 10, in <module>
    exec compile(u'open("___code___.py","w").write("# -*- coding: utf-8 -*-\\n" + _support_.preparse_worksheet_cell(base64.b64decode("aW50ZWdyYWwgKC0xL3heMiwgKHgsIDAsIDEpKQ=="),globals())+"\\n"); execfile(os.path.abspath("___code___.py"))
  File "", line 1, in <module>
    
  File "/tmp/tmp2O86lw/___code___.py", line 3, in <module>
    exec compile(u'integral (-_sage_const_1 /x**_sage_const_2 , (x, _sage_const_0 , _sage_const_1 ))
  File "", line 1, in <module>
    
  File "/opt/SageMath/local/lib/python2.7/site-packages/sage/misc/functional.py", line 753, in integral
    return x.integral(*args, **kwds)
  File "sage/symbolic/expression.pyx", line 12366, in sage.symbolic.expression.Expression.integral (build/cythonized/sage/symbolic/expression.cpp:69760)
  File "/opt/SageMath/local/lib/python2.7/site-packages/sage/symbolic/integration/integral.py", line 820, in integrate
    return definite_integral(expression, v, a, b, hold=hold)
  File "sage/symbolic/function.pyx", line 998, in sage.symbolic.function.BuiltinFunction.__call__ (build/cythonized/sage/symbolic/function.cpp:11922)
  File "sage/symbolic/function.pyx", line 487, in sage.symbolic.function.Function.__call__ (build/cythonized/sage/symbolic/function.cpp:6848)
  File "sage/symbolic/function.pyx", line 1086, in sage.symbolic.function.BuiltinFunction._evalf_or_eval_ (build/cythonized/sage/symbolic/function.cpp:13207)
  File "/opt/SageMath/local/lib/python2.7/site-packages/sage/symbolic/integration/integral.py", line 180, in _eval_
    return integrator(*args)
  File "/opt/SageMath/local/lib/python2.7/site-packages/sage/symbolic/integration/external.py", line 34, in maxima_integrator
    result = maxima.sr_integral(expression, v, a, b)
  File "/opt/SageMath/local/lib/python2.7/site-packages/sage/interfaces/maxima_lib.py", line 811, in sr_integral
    raise ValueError("Integral is divergent.")
ValueError: Integral is divergent.

Numerička integracija

Postoje funkcije integrali kojih se ne mogu točno izračunati (ili ih barem SageMath ne zna izračunati), iako je lako vidjeti da ploštine ispod njihovih grafova postoje; primjerice:

integral (x^x, (x, 0, 2))

$\newcommand{\Bold}[1]{\mathbf{#1}}\int_{0}^{2} x^{x}\,{d x}$

plot (x^x, (x, 0, 2), fill = True, figsize = 6)

Takve se funkcije mogu integrirati numerički:

area, err = numerical_integral (x^x, 0, 2)
area; err

$\newcommand{\Bold}[1]{\mathbf{#1}}2.8338767401244733$

$\newcommand{\Bold}[1]{\mathbf{#1}}1.6079092247025148 \times 10^{-06}$

rezultat su dva broja: ploština površine „ispod” grafa funkcija i, budući da je numerička integracija približna, ocjena pogreške — apsolutna vrijednost razlike između „stvarne” i izračunane ploštine nije veća od tog broja; drugim riječima, stvarna je ploština neka vrijednost iz intervala

[area - err, area + err]

$\newcommand{\Bold}[1]{\mathbf{#1}}\left[2.8338751322152484, 2.833878348033698\right]$

Naravno, numerički se mogu integrirati i funkcije čiji su točni integrali poznati:

area, err = numerical_integral (-1/x^2, 1, oo)
area; err

$\newcommand{\Bold}[1]{\mathbf{#1}}-1.0$

$\newcommand{\Bold}[1]{\mathbf{#1}}1.1102230246251565 \times 10^{-14}$

točna vrijednost, vidjeli smo, jest $-1$ ;

area, err = numerical_integral (log(x), 0, 1)
area; err

$\newcommand{\Bold}[1]{\mathbf{#1}}-0.9999999984543851$

$\newcommand{\Bold}[1]{\mathbf{#1}}6.984563559375666 \times 10^{-07}$

točna je vrijednost $-1$ ;

area, err = numerical_integral (sin(2*x) * sin(x/4), 0, 4*pi)
area; err; [area - err, area + err]

$\newcommand{\Bold}[1]{\mathbf{#1}}1.0560674032479055 \times 10^{-15}$

$\newcommand{\Bold}[1]{\mathbf{#1}}5.596795815141414 \times 10^{-14}$

$\newcommand{\Bold}[1]{\mathbf{#1}}\left[-5.491189074816624 \times 10^{-14}, 5.702402555466204 \times 10^{-14}\right]$

točna je vrijednost $0$ .

Pri numeričkoj integraciji treba biti oprezan:

numerical_integral (-1/x, 0, 1)

$\newcommand{\Bold}[1]{\mathbf{#1}}\left(-69.45462466669275, 13.11226951649312\right)$

numerical_integral (-1/x, 1, oo)

$\newcommand{\Bold}[1]{\mathbf{#1}}\left(-65.94931131932763, 8.156214940519742\right)$

Neodređeni integrali

Obrnuti problem tangente: iz nagiba tangenata krivulje treba odrediti tu krivulju

f(x) = x
f

$\newcommand{\Bold}[1]{\mathbf{#1}}x \ {\mapsto}\ x$

Funkcijom $f$ zadano je polje smjerova ili polje nagibâ:

var ('y')
psf = plot_slope_field (f, (x, -2, 2), (y, -2, 2), plot_points = 41, color = 'red')
psf.show (figsize = 6)

F(x) = integral (f, x)
F

$\newcommand{\Bold}[1]{\mathbf{#1}}x \ {\mapsto}\ \frac{1}{2} \, x^{2}$

diff (F, x)

$\newcommand{\Bold}[1]{\mathbf{#1}}x \ {\mapsto}\ x$

pF = plot (F, (x, -2, 2))
show (pF + psf, ymin = -2, ymax = 2, figsize = 6)

Za razliku od određenoga integrala, koji je broj, neodređeni integral $F = \displaystyle\int\!f(x)\,dx$ je funkcija. Primitivna funkcija ili neodređeni integral funkcije $f$ je funkcija $F$ čija je derivacija funkcija $f$ : $F' = f$ .

var ('C')
F + C

$\newcommand{\Bold}[1]{\mathbf{#1}}x \ {\mapsto}\ \frac{1}{2} \, x^{2} + C$

diff (F + C, x)

$\newcommand{\Bold}[1]{\mathbf{#1}}x \ {\mapsto}\ x$

pF = [plot (F + c, (x, -2, 2)) for c in srange (-4., 2.1, 0.1)]
show (sum (pF) + psf, ymin = -2, ymax = 2, figsize = 6)

Ako je $F$ primitivna funkcija funkcije $f$ , onda su njezine primitivne funkcije i sve funkcije $F + C$ , gdje je $C$ bilo koja konstanta. I, s druge strane, sve primitivne funkcije funkcije $f$ oblika su $F + C$ .

f(x) = x^2
f

$\newcommand{\Bold}[1]{\mathbf{#1}}x \ {\mapsto}\ x^{2}$

F(x) = integral (f, x)
F + C

$\newcommand{\Bold}[1]{\mathbf{#1}}x \ {\mapsto}\ \frac{1}{3} \, x^{3} + C$

diff (F + C, x)

$\newcommand{\Bold}[1]{\mathbf{#1}}x \ {\mapsto}\ x^{2}$

psf = plot_slope_field (f, (x, -2, 2), (y, -2, 2), plot_points = 41, color = 'red')
pF = [plot (F + c, (x, -2, 2)) for c in srange (-5., 5., 0.1)]
show (sum (pF) + psf, ymin = -2, ymax = 2, figsize = 6)

f(x) = log(x)
f

$\newcommand{\Bold}[1]{\mathbf{#1}}x \ {\mapsto}\ \log\left(x\right)$

F(x) = integral (f, x)
F + C

$\newcommand{\Bold}[1]{\mathbf{#1}}x \ {\mapsto}\ x \log\left(x\right) + C - x$

psf = plot_slope_field (f, (x, 0, 2), (y, -1, 1), plot_points = 41, color = 'red')
pF = [plot (F + c, (x, 0, 2)) for c in srange (-1, 2.1, 0.05)]
show (sum (pF) + psf, ymin = -1, ymax = 1, figsize = 6)

Divergentnost određenoga integrala (za neke granice) ne znači da se integral ne može simbolički riješiti:

integral (-1/x, x, 0, 1)

Traceback (click to the left of this block for traceback)
...
ValueError: Integral is divergent.

Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
  File "_sage_input_117.py", line 10, in <module>
    exec compile(u'open("___code___.py","w").write("# -*- coding: utf-8 -*-\\n" + _support_.preparse_worksheet_cell(base64.b64decode("aW50ZWdyYWwgKC0xL3gsIHgsIDAsIDEp"),globals())+"\\n"); execfile(os.path.abspath("___code___.py"))
  File "", line 1, in <module>
    
  File "/tmp/tmpwrvXvq/___code___.py", line 3, in <module>
    exec compile(u'integral (-_sage_const_1 /x, x, _sage_const_0 , _sage_const_1 )
  File "", line 1, in <module>
    
  File "/opt/SageMath/local/lib/python2.7/site-packages/sage/misc/functional.py", line 753, in integral
    return x.integral(*args, **kwds)
  File "sage/symbolic/expression.pyx", line 12366, in sage.symbolic.expression.Expression.integral (build/cythonized/sage/symbolic/expression.cpp:69760)
  File "/opt/SageMath/local/lib/python2.7/site-packages/sage/symbolic/integration/integral.py", line 820, in integrate
    return definite_integral(expression, v, a, b, hold=hold)
  File "sage/symbolic/function.pyx", line 998, in sage.symbolic.function.BuiltinFunction.__call__ (build/cythonized/sage/symbolic/function.cpp:11922)
  File "sage/symbolic/function.pyx", line 487, in sage.symbolic.function.Function.__call__ (build/cythonized/sage/symbolic/function.cpp:6848)
  File "sage/symbolic/function.pyx", line 1086, in sage.symbolic.function.BuiltinFunction._evalf_or_eval_ (build/cythonized/sage/symbolic/function.cpp:13207)
  File "/opt/SageMath/local/lib/python2.7/site-packages/sage/symbolic/integration/integral.py", line 180, in _eval_
    return integrator(*args)
  File "/opt/SageMath/local/lib/python2.7/site-packages/sage/symbolic/integration/external.py", line 34, in maxima_integrator
    result = maxima.sr_integral(expression, v, a, b)
  File "/opt/SageMath/local/lib/python2.7/site-packages/sage/interfaces/maxima_lib.py", line 811, in sr_integral
    raise ValueError("Integral is divergent.")
ValueError: Integral is divergent.

integral (-1/x, x)

$\newcommand{\Bold}[1]{\mathbf{#1}}-\log\left(x\right)$

psf = plot_slope_field (-1/x, (x, 0.02, 2), (y, -1, 0.5), plot_points = 31, color = 'red')
pF = [plot (-log(x) + c, (x, 0.02, 2)) for c in srange (-5., 1.5, 0.05)]
show (sum (pF) + psf, ymin = -1, ymax = 0.5, figsize = 6)

Jedna primjena u mehanici

Newtonova je kinematička inačica obrnutoga problema tangente: „Ako je zadana brzina gibanja u kojigod vremenski čas, naći duljinu puta opisana u određenu vremenu”. Pri slobodnomu je padu, primjerice:

var ('t')
v(t) = 9.81 * t
v

$\newcommand{\Bold}[1]{\mathbf{#1}}t \ {\mapsto}\ 9.81000000000000 \, t$

s(t) = integral (v, t)
s

$\newcommand{\Bold}[1]{\mathbf{#1}}t \ {\mapsto}\ 4.905 \, t^{2}$

Veza određenoga integrala i primitivne funkcije (Newton–Leibnizova formula)

Ako je $F$ primitivna funkcija funkcije $f$ , onda je

$\displaystyle \int_a^b f(x)\,dx \:=\: F(b) - F(a)$ .

f(x) = sin(x) + 1/2*sin(3*x)
a = 0.425
b = 2.625
F(x) = integral (f(x), x)
F

$\newcommand{\Bold}[1]{\mathbf{#1}}x \ {\mapsto}\ -\frac{1}{6} \, \cos\left(3 \, x\right) - \cos\left(x\right)$

F(b) - F(a)

$\newcommand{\Bold}[1]{\mathbf{#1}}1.83263233167811$

integral (f(x), x, a, b)

$\newcommand{\Bold}[1]{\mathbf{#1}}1.8326323316781108$

F(x) = integral (-1/x, x)
F

$\newcommand{\Bold}[1]{\mathbf{#1}}x \ {\mapsto}\ -\log\left(x\right)$

F(1) - F(0)

$\newcommand{\Bold}[1]{\mathbf{#1}}-\infty$

integral (-1/x, x, 0, 1)

Traceback (click to the left of this block for traceback)
...
ValueError: Integral is divergent.

Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
  File "_sage_input_130.py", line 10, in <module>
    exec compile(u'open("___code___.py","w").write("# -*- coding: utf-8 -*-\\n" + _support_.preparse_worksheet_cell(base64.b64decode("aW50ZWdyYWwgKC0xL3gsIHgsIDAsIDEp"),globals())+"\\n"); execfile(os.path.abspath("___code___.py"))
  File "", line 1, in <module>
    
  File "/tmp/tmpAuFAKc/___code___.py", line 3, in <module>
    exec compile(u'integral (-_sage_const_1 /x, x, _sage_const_0 , _sage_const_1 )
  File "", line 1, in <module>
    
  File "/opt/SageMath/local/lib/python2.7/site-packages/sage/misc/functional.py", line 753, in integral
    return x.integral(*args, **kwds)
  File "sage/symbolic/expression.pyx", line 12366, in sage.symbolic.expression.Expression.integral (build/cythonized/sage/symbolic/expression.cpp:69760)
  File "/opt/SageMath/local/lib/python2.7/site-packages/sage/symbolic/integration/integral.py", line 820, in integrate
    return definite_integral(expression, v, a, b, hold=hold)
  File "sage/symbolic/function.pyx", line 998, in sage.symbolic.function.BuiltinFunction.__call__ (build/cythonized/sage/symbolic/function.cpp:11922)
  File "sage/symbolic/function.pyx", line 487, in sage.symbolic.function.Function.__call__ (build/cythonized/sage/symbolic/function.cpp:6848)
  File "sage/symbolic/function.pyx", line 1086, in sage.symbolic.function.BuiltinFunction._evalf_or_eval_ (build/cythonized/sage/symbolic/function.cpp:13207)
  File "/opt/SageMath/local/lib/python2.7/site-packages/sage/symbolic/integration/integral.py", line 180, in _eval_
    return integrator(*args)
  File "/opt/SageMath/local/lib/python2.7/site-packages/sage/symbolic/integration/external.py", line 34, in maxima_integrator
    result = maxima.sr_integral(expression, v, a, b)
  File "/opt/SageMath/local/lib/python2.7/site-packages/sage/interfaces/maxima_lib.py", line 811, in sr_integral
    raise ValueError("Integral is divergent.")
ValueError: Integral is divergent.

F(oo) - F(1)

$\newcommand{\Bold}[1]{\mathbf{#1}}-\infty$

integral (-1/x, x, 1, oo)

Traceback (click to the left of this block for traceback)
...
ValueError: Integral is divergent.

Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
  File "_sage_input_131.py", line 10, in <module>
    exec compile(u'open("___code___.py","w").write("# -*- coding: utf-8 -*-\\n" + _support_.preparse_worksheet_cell(base64.b64decode("aW50ZWdyYWwgKC0xL3gsIHgsIDEsIG9vKQ=="),globals())+"\\n"); execfile(os.path.abspath("___code___.py"))
  File "", line 1, in <module>
    
  File "/tmp/tmpox7wxd/___code___.py", line 3, in <module>
    exec compile(u'integral (-_sage_const_1 /x, x, _sage_const_1 , oo)
  File "", line 1, in <module>
    
  File "/opt/SageMath/local/lib/python2.7/site-packages/sage/misc/functional.py", line 753, in integral
    return x.integral(*args, **kwds)
  File "sage/symbolic/expression.pyx", line 12366, in sage.symbolic.expression.Expression.integral (build/cythonized/sage/symbolic/expression.cpp:69760)
  File "/opt/SageMath/local/lib/python2.7/site-packages/sage/symbolic/integration/integral.py", line 820, in integrate
    return definite_integral(expression, v, a, b, hold=hold)
  File "sage/symbolic/function.pyx", line 998, in sage.symbolic.function.BuiltinFunction.__call__ (build/cythonized/sage/symbolic/function.cpp:11922)
  File "sage/symbolic/function.pyx", line 487, in sage.symbolic.function.Function.__call__ (build/cythonized/sage/symbolic/function.cpp:6848)
  File "sage/symbolic/function.pyx", line 1086, in sage.symbolic.function.BuiltinFunction._evalf_or_eval_ (build/cythonized/sage/symbolic/function.cpp:13207)
  File "/opt/SageMath/local/lib/python2.7/site-packages/sage/symbolic/integration/integral.py", line 180, in _eval_
    return integrator(*args)
  File "/opt/SageMath/local/lib/python2.7/site-packages/sage/symbolic/integration/external.py", line 34, in maxima_integrator
    result = maxima.sr_integral(expression, v, a, b)
  File "/opt/SageMath/local/lib/python2.7/site-packages/sage/interfaces/maxima_lib.py", line 811, in sr_integral
    raise ValueError("Integral is divergent.")
ValueError: Integral is divergent.

F(x) = integral (-1/x^2, x)
F

$\newcommand{\Bold}[1]{\mathbf{#1}}x \ {\mapsto}\ \frac{1}{x}$

F(oo) - F(1)

$\newcommand{\Bold}[1]{\mathbf{#1}}-1$

Primjena pretpostavaka

var ('n')
integral (x^n, x)

Traceback (click to the left of this block for traceback)
...
Is n equal to -1?

Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
  File "_sage_input_134.py", line 10, in <module>
    exec compile(u'open("___code___.py","w").write("# -*- coding: utf-8 -*-\\n" + _support_.preparse_worksheet_cell(base64.b64decode("dmFyICgnbicpCmludGVncmFsICh4Xm4sIHgp"),globals())+"\\n"); execfile(os.path.abspath("___code___.py"))
  File "", line 1, in <module>
    
  File "/tmp/tmpfE8eHx/___code___.py", line 3, in <module>
    exec compile(u'integral (x**n, x)
  File "", line 1, in <module>
    
  File "/opt/SageMath/local/lib/python2.7/site-packages/sage/misc/functional.py", line 753, in integral
    return x.integral(*args, **kwds)
  File "sage/symbolic/expression.pyx", line 12366, in sage.symbolic.expression.Expression.integral (build/cythonized/sage/symbolic/expression.cpp:69760)
  File "/opt/SageMath/local/lib/python2.7/site-packages/sage/symbolic/integration/integral.py", line 818, in integrate
    return indefinite_integral(expression, v, hold=hold)
  File "sage/symbolic/function.pyx", line 998, in sage.symbolic.function.BuiltinFunction.__call__ (build/cythonized/sage/symbolic/function.cpp:11922)
  File "sage/symbolic/function.pyx", line 492, in sage.symbolic.function.Function.__call__ (build/cythonized/sage/symbolic/function.cpp:6949)
  File "/opt/SageMath/local/lib/python2.7/site-packages/sage/symbolic/integration/integral.py", line 90, in _eval_
    return integrator(f, x)
  File "/opt/SageMath/local/lib/python2.7/site-packages/sage/symbolic/integration/external.py", line 32, in maxima_integrator
    result = maxima.sr_integral(expression,v)
  File "/opt/SageMath/local/lib/python2.7/site-packages/sage/interfaces/maxima_lib.py", line 813, in sr_integral
    self._missing_assumption(s)
  File "/opt/SageMath/local/lib/python2.7/site-packages/sage/interfaces/maxima_lib.py", line 1049, in _missing_assumption
    raise ValueError(outstr)
ValueError: Computation failed since Maxima requested additional constraints; using the 'assume' command before evaluation *may* help (example of legal syntax is 'assume(n>0)', see `assume?` for more details)
Is n equal to -1?

assume (n == -1)
assumptions()

$\newcommand{\Bold}[1]{\mathbf{#1}}\left[n = \left(-1\right)\right]$

integral (x^n, x)

$\newcommand{\Bold}[1]{\mathbf{#1}}\log\left(x\right)$

forget()
assume (n != -1)
assumptions()

$\newcommand{\Bold}[1]{\mathbf{#1}}\left[n \neq \left(-1\right)\right]$

integral (x^n, x)

$\newcommand{\Bold}[1]{\mathbf{#1}}\frac{x^{n + 1}}{n + 1}$

forget()
assumptions()

$\newcommand{\Bold}[1]{\mathbf{#1}}\left[\right]$

Još jedan primjer:

var('a b')
f(x) = 1/(x^3 * (a+b*x)^(1/3))
f

$\newcommand{\Bold}[1]{\mathbf{#1}}x \ {\mapsto}\ \frac{1}{{\left(b x + a\right)}^{\frac{1}{3}} x^{3}}$

integral (f(x), x)

Traceback (click to the left of this block for traceback)
...
Is a positive or negative?

Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
  File "_sage_input_141.py", line 10, in <module>
    exec compile(u'open("___code___.py","w").write("# -*- coding: utf-8 -*-\\n" + _support_.preparse_worksheet_cell(base64.b64decode("aW50ZWdyYWwgKGYoeCksIHgp"),globals())+"\\n"); execfile(os.path.abspath("___code___.py"))
  File "", line 1, in <module>
    
  File "/tmp/tmpgaIhNJ/___code___.py", line 2, in <module>
    exec compile(u'integral (f(x), x)
  File "", line 1, in <module>
    
  File "/opt/SageMath/local/lib/python2.7/site-packages/sage/misc/functional.py", line 753, in integral
    return x.integral(*args, **kwds)
  File "sage/symbolic/expression.pyx", line 12366, in sage.symbolic.expression.Expression.integral (build/cythonized/sage/symbolic/expression.cpp:69760)
  File "/opt/SageMath/local/lib/python2.7/site-packages/sage/symbolic/integration/integral.py", line 818, in integrate
    return indefinite_integral(expression, v, hold=hold)
  File "sage/symbolic/function.pyx", line 998, in sage.symbolic.function.BuiltinFunction.__call__ (build/cythonized/sage/symbolic/function.cpp:11922)
  File "sage/symbolic/function.pyx", line 492, in sage.symbolic.function.Function.__call__ (build/cythonized/sage/symbolic/function.cpp:6949)
  File "/opt/SageMath/local/lib/python2.7/site-packages/sage/symbolic/integration/integral.py", line 90, in _eval_
    return integrator(f, x)
  File "/opt/SageMath/local/lib/python2.7/site-packages/sage/symbolic/integration/external.py", line 32, in maxima_integrator
    result = maxima.sr_integral(expression,v)
  File "/opt/SageMath/local/lib/python2.7/site-packages/sage/interfaces/maxima_lib.py", line 813, in sr_integral
    self._missing_assumption(s)
  File "/opt/SageMath/local/lib/python2.7/site-packages/sage/interfaces/maxima_lib.py", line 1049, in _missing_assumption
    raise ValueError(outstr)
ValueError: Computation failed since Maxima requested additional constraints; using the 'assume' command before evaluation *may* help (example of legal syntax is 'assume(a>0)', see `assume?` for more details)
Is a positive or negative?

assume (a > 0)
integral (f(x), x)

$\newcommand{\Bold}[1]{\mathbf{#1}}\frac{2 \, \sqrt{3} b^{2} \arctan\left(\frac{\sqrt{3} {\left(2 \, {\left(b x + a\right)}^{\frac{1}{3}} + a^{\frac{1}{3}}\right)}}{3 \, a^{\frac{1}{3}}}\right)}{9 \, a^{\frac{7}{3}}} - \frac{b^{2} \log\left({\left(b x + a\right)}^{\frac{2}{3}} + {\left(b x + a\right)}^{\frac{1}{3}} a^{\frac{1}{3}} + a^{\frac{2}{3}}\right)}{9 \, a^{\frac{7}{3}}} + \frac{2 \, b^{2} \log\left({\left(b x + a\right)}^{\frac{1}{3}} - a^{\frac{1}{3}}\right)}{9 \, a^{\frac{7}{3}}} + \frac{4 \, {\left(b x + a\right)}^{\frac{5}{3}} b^{2} - 7 \, {\left(b x + a\right)}^{\frac{2}{3}} a b^{2}}{6 \, {\left({\left(b x + a\right)}^{2} a^{2} - 2 \, {\left(b x + a\right)} a^{3} + a^{4}\right)}}$

_.simplify_full()

$\newcommand{\Bold}[1]{\mathbf{#1}}-\frac{\sqrt{3} {\left(2 \, \sqrt{3} b^{2} x^{2} \log\left({\left(b x + a\right)}^{\frac{2}{3}} + {\left(b x + a\right)}^{\frac{1}{3}} a^{\frac{1}{3}} + a^{\frac{2}{3}}\right) - 4 \, \sqrt{3} b^{2} x^{2} \log\left({\left(b x + a\right)}^{\frac{1}{3}} - a^{\frac{1}{3}}\right) - 12 \, b^{2} x^{2} \arctan\left(\frac{\sqrt{3} {\left(2 \, {\left(b x + a\right)}^{\frac{1}{3}} + a^{\frac{1}{3}}\right)}}{3 \, a^{\frac{1}{3}}}\right) - 3 \, {\left(4 \, \sqrt{3} b x - 3 \, \sqrt{3} a\right)} {\left(b x + a\right)}^{\frac{2}{3}} a^{\frac{1}{3}}\right)}}{54 \, a^{\frac{7}{3}} x^{2}}$

forget()
assume (a < 0)
integral (f(x), x)

$\newcommand{\Bold}[1]{\mathbf{#1}}\frac{2 \, \sqrt{3} b^{2} \arctan\left(\frac{\sqrt{3} {\left(2 \, {\left(b x + a\right)}^{\frac{1}{3}} - \left(-a\right)^{\frac{1}{3}}\right)}}{3 \, \left(-a\right)^{\frac{1}{3}}}\right)}{9 \, \left(-a\right)^{\frac{1}{3}} a^{2}} + \frac{b^{2} \log\left({\left(b x + a\right)}^{\frac{2}{3}} - {\left(b x + a\right)}^{\frac{1}{3}} \left(-a\right)^{\frac{1}{3}} + \left(-a\right)^{\frac{2}{3}}\right)}{9 \, \left(-a\right)^{\frac{1}{3}} a^{2}} - \frac{2 \, b^{2} \log\left({\left(b x + a\right)}^{\frac{1}{3}} + \left(-a\right)^{\frac{1}{3}}\right)}{9 \, \left(-a\right)^{\frac{1}{3}} a^{2}} + \frac{4 \, {\left(b x + a\right)}^{\frac{5}{3}} b^{2} - 7 \, {\left(b x + a\right)}^{\frac{2}{3}} a b^{2}}{6 \, {\left({\left(b x + a\right)}^{2} a^{2} - 2 \, {\left(b x + a\right)} a^{3} + a^{4}\right)}}$

_.simplify_full()

$\newcommand{\Bold}[1]{\mathbf{#1}}\frac{\sqrt{3} {\left(2 \, \sqrt{3} b^{2} x^{2} \log\left({\left(b x + a\right)}^{\frac{2}{3}} - {\left(b x + a\right)}^{\frac{1}{3}} \left(-a\right)^{\frac{1}{3}} + \left(-a\right)^{\frac{2}{3}}\right) - 4 \, \sqrt{3} b^{2} x^{2} \log\left({\left(b x + a\right)}^{\frac{1}{3}} + \left(-a\right)^{\frac{1}{3}}\right) + 12 \, b^{2} x^{2} \arctan\left(\frac{\sqrt{3} {\left(2 \, {\left(b x + a\right)}^{\frac{1}{3}} - \left(-a\right)^{\frac{1}{3}}\right)}}{3 \, \left(-a\right)^{\frac{1}{3}}}\right) + 3 \, {\left(4 \, \sqrt{3} b x - 3 \, \sqrt{3} a\right)} {\left(b x + a\right)}^{\frac{2}{3}} \left(-a\right)^{\frac{1}{3}}\right)}}{54 \, \left(-a\right)^{\frac{1}{3}} a^{2} x^{2}}$

forget()
assume (a == 0)
integral (f(x), x)

$\newcommand{\Bold}[1]{\mathbf{#1}}-\frac{2 \, b^{2}}{3 \, {\left(2 \, {\left(b x + a\right)}^{\frac{1}{3}} a^{2} - \left(-a\right)^{\frac{1}{3}} a^{2}\right)}} + \frac{2 \, b^{2} \log\left(2 \, {\left(b x + a\right)}^{\frac{1}{3}} - \left(-a\right)^{\frac{1}{3}}\right)}{9 \, \left(-a\right)^{\frac{1}{3}} a^{2}} - \frac{2 \, b^{2} \log\left({\left(b x + a\right)}^{\frac{1}{3}} + \left(-a\right)^{\frac{1}{3}}\right)}{9 \, \left(-a\right)^{\frac{1}{3}} a^{2}} + \frac{4 \, {\left(b x + a\right)}^{\frac{5}{3}} b^{2} - 7 \, {\left(b x + a\right)}^{\frac{2}{3}} a b^{2}}{6 \, {\left({\left(b x + a\right)}^{2} a^{2} - 2 \, {\left(b x + a\right)} a^{3} + a^{4}\right)}}$

_.simplify_full()

Traceback (click to the left of this block for traceback)
...
TypeError: ECL says: Error executing code in Maxima: expt: undefined: 0 to a
negative exponent.

Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
  File "_sage_input_152.py", line 10, in <module>
    exec compile(u'open("___code___.py","w").write("# -*- coding: utf-8 -*-\\n" + _support_.preparse_worksheet_cell(base64.b64decode("Xy5zaW1wbGlmeV9mdWxsKCk="),globals())+"\\n"); execfile(os.path.abspath("___code___.py"))
  File "", line 1, in <module>
    
  File "/tmp/tmpzLow5W/___code___.py", line 2, in <module>
    exec compile(u'_.simplify_full()
  File "", line 1, in <module>
    
  File "sage/symbolic/expression.pyx", line 9926, in sage.symbolic.expression.Expression.simplify_full (build/cythonized/sage/symbolic/expression.cpp:54830)
  File "sage/symbolic/expression.pyx", line 10074, in sage.symbolic.expression.Expression.simplify_rectform (build/cythonized/sage/symbolic/expression.cpp:56767)
  File "sage/symbolic/expression.pyx", line 9758, in sage.symbolic.expression.Expression.rectform (build/cythonized/sage/symbolic/expression.cpp:54307)
  File "/opt/SageMath/local/lib/python2.7/site-packages/sage/symbolic/maxima_wrapper.py", line 32, in __call__
    **kwds).sage()
  File "/opt/SageMath/local/lib/python2.7/site-packages/sage/interfaces/interface.py", line 655, in __call__
    return self._obj.parent().function_call(self._name, [self._obj] + list(args), kwds)
  File "/opt/SageMath/local/lib/python2.7/site-packages/sage/interfaces/interface.py", line 576, in function_call
    return self.new(s)
  File "/opt/SageMath/local/lib/python2.7/site-packages/sage/interfaces/interface.py", line 345, in new
    return self(code)
  File "/opt/SageMath/local/lib/python2.7/site-packages/sage/interfaces/interface.py", line 280, in __call__
    return cls(self, x, name=name)
  File "/opt/SageMath/local/lib/python2.7/site-packages/sage/interfaces/interface.py", line 695, in __init__
    raise TypeError(x)
TypeError: ECL says: Error executing code in Maxima: expt: undefined: 0 to a negative exponent.

integral (f(x), x).subs (a = 0)

Traceback (click to the left of this block for traceback)
...
ValueError: power::eval(): division by zero

Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
  File "_sage_input_153.py", line 10, in <module>
    exec compile(u'open("___code___.py","w").write("# -*- coding: utf-8 -*-\\n" + _support_.preparse_worksheet_cell(base64.b64decode("aW50ZWdyYWwgKGYoeCksIHgpLnN1YnMgKGEgPSAwKQ=="),globals())+"\\n"); execfile(os.path.abspath("___code___.py"))
  File "", line 1, in <module>
    
  File "/tmp/tmpf0lKr8/___code___.py", line 3, in <module>
    exec compile(u'integral (f(x), x).subs (a = _sage_const_0 )
  File "", line 1, in <module>
    
  File "sage/symbolic/expression.pyx", line 5299, in sage.symbolic.expression.Expression.substitute (build/cythonized/sage/symbolic/expression.cpp:32803)
ValueError: power::eval(): division by zero

forget()
assumptions()

$\newcommand{\Bold}[1]{\mathbf{#1}}\left[\right]$

Uvod u diferencijalne jednadžbe

Diferencijalna jednadžba je jednadžba kojom je zadana veza između neovisnih varijabli, tražene funkcije tih varijabli i njezinih derivacija po tim varijablama. Obična diferencijalna jednažba sadrži funkciju jedne varijable, njezine derivacije i tu varijabla. Najviša derivacija, koja se u diferencijalnoj jednadžbi pojavljuje, određuje njezin red.

Prigušene oscilacije (problem s početnim uvjetima)

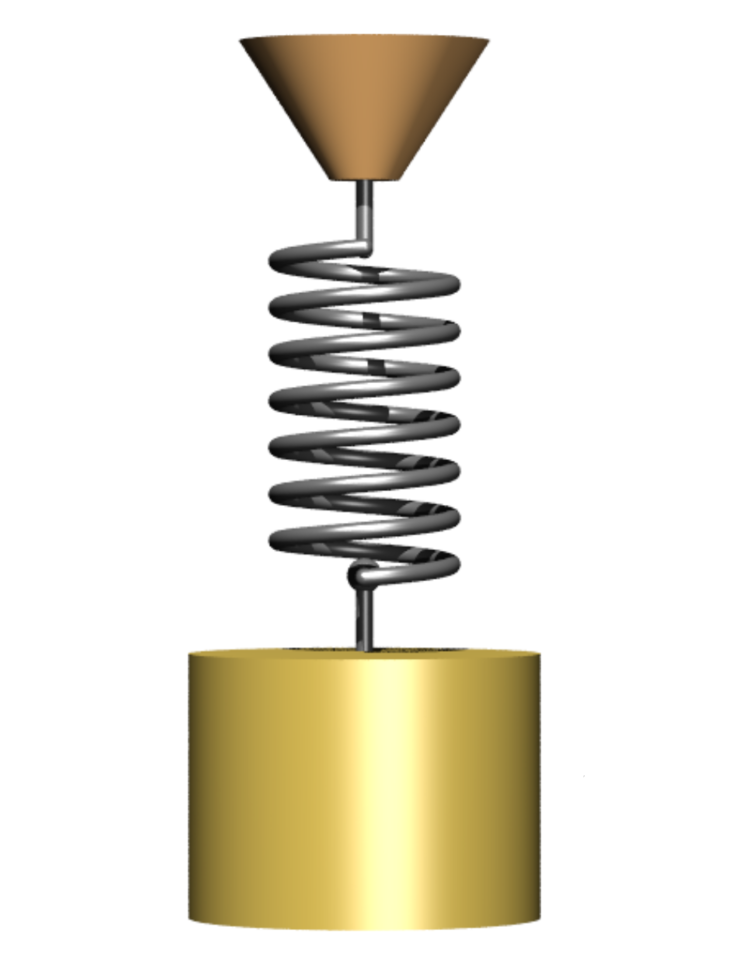
Uteg mase $m$ , koji visi na elastičnoj opruzi, povući ćemo prema dolje iz početnoga (ravnotežnog) položaja $z = 0$ u položaj $z = z_0$ . Radi promjene oblika javlja se u zavojnici elastična sila $\vec{F}_{\mathrm{e}} = F_{\mathrm{e}}\,\vec{k}$ koja je teži vratiti u početni oblik (ta je sila po intenzitetu jednaka sili kojom smo povukli uteg, ali je od nje suprotno orijentirana).

Iskustvo je pokazalo da je pri malim produljenjima i skraćenjima opruge ta sila harmonijska, što znači da joj je veličina razmjerna promjeni duljine opruge (riječ je o Hookeovu zakonu s kojim ćete se često susretati). Budući da se sila odupire promjeni duljine, bit će $F_{\mathrm{e}} = -E\, z$ , gdje je $E>0$ faktor proporcionalnosti. Ako pustimo uteg, počet će se pod djelovanjem sile $\vec{F}_{\mathrm{e}}$ gibati po vertikalnom pravcu. Zrak kroz koji se uteg giba i unutarnje trenje u oprugi pružaju otpor gibanju — prigušuju ga. Sila viskoznoga prigušenja proporcionalna je brzini gibanja: $\vec{F}_{\mathrm{v}} = F_{\mathrm{v}}\,\vec{k} = -c\, v\,\vec{k}$ .

Gibanje će biti opisano funkcijom $z : t \mapsto z(t)$ . Budući da je $z$ funkcija vremena $t$ , funkcije vremena bit će i vrijednosti $F_{\mathrm{e}}$ i $F_{\mathrm{v}}$ sila $\vec{F}_{\mathrm{e}}$ i $\vec{F}_{\mathrm{v}}$ . Prema drugom je Newtonovu zakonu

$m\,a(t) = F_{\mathrm{v}}(t) + F_{\mathrm{e}}(t)$ , odnosno, $m\,a(t) = -c\, v(t) -E\,z(t)$ , odnosno $m\,\ddot{z}(t) = -c\,\dot{z}(t) -E\,z(t)$ .

Dobivena diferencijalna jednadžba drugoga je reda.

Definicija diferencijalne jednadžbe:

var ('t z0 E c m')
z = function ('z')(t)
deq = m * diff (z, t, 2) == -c * diff (z, t) - E * z

Rješavanje (u nekoliko pokušaja):

zz(t) = desolve (deq, z)

Traceback (click to the left of this block for traceback)
...
ValueError: Unable to determine independent variable, please specify.

Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
  File "_sage_input_159.py", line 10, in <module>
    exec compile(u'open("___code___.py","w").write("# -*- coding: utf-8 -*-\\n" + _support_.preparse_worksheet_cell(base64.b64decode("enoodCkgPSBkZXNvbHZlIChkZXEsIHop"),globals())+"\\n"); execfile(os.path.abspath("___code___.py"))
  File "", line 1, in <module>
    
  File "/tmp/tmpmaBwHG/___code___.py", line 2, in <module>
    exec compile(u'__tmp__=var("t"); zz = symbolic_expression(desolve (deq, z)).function(t)
  File "", line 1, in <module>
    
  File "/opt/SageMath/local/lib/python2.7/site-packages/sage/calculus/desolvers.py", line 453, in desolve
    raise ValueError("Unable to determine independent variable, please specify.")
ValueError: Unable to determine independent variable, please specify.

... — independent variable (neovisna varijabla: $z$ je funkcija neovisne varijable $t$ ):

zz(t) = desolve (deq, z, ivar = t)

Traceback (click to the left of this block for traceback)
...
Is 4*E*m-c^2 positive, negative or zero?

Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
  File "_sage_input_160.py", line 10, in <module>
    exec compile(u'open("___code___.py","w").write("# -*- coding: utf-8 -*-\\n" + _support_.preparse_worksheet_cell(base64.b64decode("enoodCkgPSBkZXNvbHZlIChkZXEsIHosIGl2YXIgPSB0KQ=="),globals())+"\\n"); execfile(os.path.abspath("___code___.py"))
  File "", line 1, in <module>
    
  File "/tmp/tmp7wcEax/___code___.py", line 2, in <module>
    exec compile(u'__tmp__=var("t"); zz = symbolic_expression(desolve (deq, z, ivar = t)).function(t)
  File "", line 1, in <module>
    
  File "/opt/SageMath/local/lib/python2.7/site-packages/sage/calculus/desolvers.py", line 467, in desolve
    soln = P(cmd)
  File "/opt/SageMath/local/lib/python2.7/site-packages/sage/interfaces/interface.py", line 280, in __call__
    return cls(self, x, name=name)
  File "/opt/SageMath/local/lib/python2.7/site-packages/sage/interfaces/interface.py", line 695, in __init__
    raise TypeError(x)
TypeError: Computation failed since Maxima requested additional constraints; using the 'assume' command before evaluation *may* help (example of legal syntax is 'assume(4*E*m-c^2>0)', see `assume?` for more details)
Is 4*E*m-c^2 positive, negative or zero?

Priroda rješenja ovisi o tome je li $4\,m\,E > c^2$ , $4\,m\,E = c^2$ ili $4\,m\,E < c^2$ . U prvom je slučaju gibanje oscilatorno, a u druga dva nije.

Slabo prigušenje:

forget()
assume (4*m*E > c^2)
assumptions()

$\newcommand{\Bold}[1]{\mathbf{#1}}\left[4 \, E m > c^{2}\right]$

z1(t) = desolve (deq, z, ivar = t)
z1

$\newcommand{\Bold}[1]{\mathbf{#1}}t \ {\mapsto}\ {\left(K_{2} \cos\left(\frac{1}{2} \, t \sqrt{-\frac{c^{2}}{m^{2}} + \frac{4 \, E}{m}}\right) + K_{1} \sin\left(\frac{1}{2} \, t \sqrt{-\frac{c^{2}}{m^{2}} + \frac{4 \, E}{m}}\right)\right)} e^{\left(-\frac{c t}{2 \, m}\right)}$

Kritično prigušenje:

forget()
assume (4*m*E == c^2)
assumptions()

$\newcommand{\Bold}[1]{\mathbf{#1}}\left[4 \, E m = c^{2}\right]$

z2(t) = desolve (deq, z, ivar = t)
z2

Traceback (click to the left of this block for traceback)
...
Is c zero or nonzero?

Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
  File "_sage_input_164.py", line 10, in <module>
    exec compile(u'open("___code___.py","w").write("# -*- coding: utf-8 -*-\\n" + _support_.preparse_worksheet_cell(base64.b64decode("ejIodCkgPSBkZXNvbHZlIChkZXEsIHosIGl2YXIgPSB0KQp6Mg=="),globals())+"\\n"); execfile(os.path.abspath("___code___.py"))
  File "", line 1, in <module>
    
  File "/tmp/tmpEjRkgX/___code___.py", line 2, in <module>
    __tmp__=var("t"); z2 = symbolic_expression(desolve (deq, z, ivar = t)).function(t)
  File "/opt/SageMath/local/lib/python2.7/site-packages/sage/calculus/desolvers.py", line 467, in desolve
    soln = P(cmd)
  File "/opt/SageMath/local/lib/python2.7/site-packages/sage/interfaces/interface.py", line 280, in __call__
    return cls(self, x, name=name)
  File "/opt/SageMath/local/lib/python2.7/site-packages/sage/interfaces/interface.py", line 695, in __init__
    raise TypeError(x)
TypeError: Computation failed since Maxima requested additional constraints; using the 'assume' command before evaluation *may* help (example of legal syntax is 'assume(c>0)', see `assume?` for more details)
Is c zero or nonzero?

assume (c != 0)
assumptions()

$\newcommand{\Bold}[1]{\mathbf{#1}}\left[4 \, E m = c^{2}, c \neq 0\right]$

z2(t) = desolve (deq, z, ivar = t)
z2

$\newcommand{\Bold}[1]{\mathbf{#1}}t \ {\mapsto}\ {\left(K_{2} t + K_{1}\right)} e^{\left(-\frac{c t}{2 \, m}\right)}$

Jako prigušenje:

forget()
assume (4*m*E < c^2)
assumptions()

$\newcommand{\Bold}[1]{\mathbf{#1}}\left[4 \, E m < c^{2}\right]$

z3(t) = desolve (deq, z, ivar = t)
z3

$\newcommand{\Bold}[1]{\mathbf{#1}}t \ {\mapsto}\ K_{2} e^{\left(-\frac{1}{2} \, t {\left(\sqrt{\frac{c^{2}}{m^{2}} - \frac{4 \, E}{m}} + \frac{c}{m}\right)}\right)} + K_{1} e^{\left(\frac{1}{2} \, t {\left(\sqrt{\frac{c^{2}}{m^{2}} - \frac{4 \, E}{m}} - \frac{c}{m}\right)}\right)}$

Uvođenje početnih uvjeta $z(0) = z_0$ i $v(0) = \dot{z}(0) = 0$ :

... ics — initial conditions

Slabo prigušenje:

forget()
assume (4*m*E > c^2)
z10(t) = desolve (deq, z, ivar = t, ics = [0, z0, 0])
z10

$\newcommand{\Bold}[1]{\mathbf{#1}}t \ {\mapsto}\ {\left(z_{0} \cos\left(\frac{1}{2} \, t \sqrt{-\frac{c^{2}}{m^{2}} + \frac{4 \, E}{m}}\right) + \frac{c z_{0} \sin\left(\frac{1}{2} \, t \sqrt{-\frac{c^{2}}{m^{2}} + \frac{4 \, E}{m}}\right)}{m \sqrt{-\frac{c^{2}}{m^{2}} + \frac{4 \, E}{m}}}\right)} e^{\left(-\frac{c t}{2 \, m}\right)}$

... primjerice, za $E = 1$ , $m = 1$ , $c = 0,\!25$ i $z_0 = -0,\!125$ (uteg smo povukli prema dolje) je

zz10 = z10.subs (E = 1, m = 1, c = 0.25, z0 = -0.125)
zz10

$\newcommand{\Bold}[1]{\mathbf{#1}}t \ {\mapsto}\ {\left(-0.125000000000000 \, \cos\left(0.992156741649222 \, t\right) - 0.0157485197087178 \, \sin\left(0.992156741649222 \, t\right)\right)} e^{\left(-0.125000000000000 \, t\right)}$

... pa je gibanje u prve 53 sekunde

lp1 = [ point ((0, zz10(t1)), size = 20, color = 'crimson') 
   + point ((t1, zz10(t1)), size = 5, color = 'crimson') 
   + plot (zz10, 0, t1, axes_labels = ['t', 'z'], figsize = 6) for t1 in srange (0.25, 53.1, 0.325) ]
ap1 = animate (lp1, xmin = 0, xmax = 53, ymin = -0.125, ymax = 0.0825)
ap1.show (delay = 8)

Kritično prigušenje:

forget()
assume (4*m*E == c^2, c != 0)
z20(t) = desolve (deq, z, ivar = t, ics = [0, z0, 0])
z20

$\newcommand{\Bold}[1]{\mathbf{#1}}t \ {\mapsto}\ \frac{1}{2} \, {\left(\frac{c t z_{0}}{m} + 2 \, z_{0}\right)} e^{\left(-\frac{c t}{2 \, m}\right)}$

... za $E = 1$ , $m = 1$ , $c = 2$ i $z_0 = -0,\!125$ je

zz20 = z20.subs (E = 1, m = 1, c = 2, z0 = -0.125)
zz20

$\newcommand{\Bold}[1]{\mathbf{#1}}t \ {\mapsto}\ \frac{1}{2} \, {\left(-0.250000000000000 \, t - 0.250000000000000\right)} e^{\left(-t\right)}$

... pa je u prvih 27 sekundi gibanje

lp2 = [ point ((0, zz20(t1)), size = 20, color = 'crimson') 
   + point ((t1, zz20(t1)), size = 5, color = 'crimson') 
   + plot (zz20, 0, t1, axes_labels = ['t', 'z'], figsize = 6) for t1 in srange (0.25, 27.1, 0.25) ]
ap2 = animate (lp2, xmin = 0, xmax = 27, ymin = -0.125, ymax = 0)
ap2.show (delay = 8)

Jako prigušenje:

forget()
assume (4*m*E < c^2)
z30(t) = desolve (deq, z, ivar = t, ics = [0, z0, 0])
z30

$\newcommand{\Bold}[1]{\mathbf{#1}}t \ {\mapsto}\ \frac{{\left(m \sqrt{\frac{c^{2}}{m^{2}} - \frac{4 \, E}{m}} - c\right)} z_{0} e^{\left(-\frac{1}{2} \, t {\left(\sqrt{\frac{c^{2}}{m^{2}} - \frac{4 \, E}{m}} + \frac{c}{m}\right)}\right)}}{2 \, m \sqrt{\frac{c^{2}}{m^{2}} - \frac{4 \, E}{m}}} + \frac{{\left(m \sqrt{\frac{c^{2}}{m^{2}} - \frac{4 \, E}{m}} + c\right)} z_{0} e^{\left(\frac{1}{2} \, t {\left(\sqrt{\frac{c^{2}}{m^{2}} - \frac{4 \, E}{m}} - \frac{c}{m}\right)}\right)}}{2 \, m \sqrt{\frac{c^{2}}{m^{2}} - \frac{4 \, E}{m}}}$

... za $E = 1$ , $m = 1$ , $c = 3$ i $z_0 = -0,\!125$ je

zz30 = z30.subs (E = 1, m = 1, c = 3, z0 = -0.125)
zz30

$\newcommand{\Bold}[1]{\mathbf{#1}}t \ {\mapsto}\ -0.0125000000000000 \, \sqrt{5} {\left(\sqrt{5} - 3\right)} e^{\left(-\frac{1}{2} \, t {\left(\sqrt{5} + 3\right)}\right)} - 0.0125000000000000 \, \sqrt{5} {\left(\sqrt{5} + 3\right)} e^{\left(\frac{1}{2} \, t {\left(\sqrt{5} - 3\right)}\right)}$

lp3 = [ point ((0, zz30(t1)), size = 20, color = 'crimson') 
   + point ((t1, zz30(t1)), size = 5, color = 'crimson') 
   + plot (zz30, 0, t1, axes_labels = ['t', 'z'], figsize = 6) for t1 in srange (0.25, 27.1, 0.25) ]
ap3 = animate (lp3, xmin = 0, xmax = 27, ymin = -0.125, ymax = 0)
ap3.show (delay = 8)

Ravnoteža užeta (problem s rubnim uvjetima)

Diferencijalna je ravnoteže užeta obješenoga u krajnjim točkama

$z''(x) = -\!\dfrac{q(x)}{H}$ ,

gdje su $q$ funkcija kojom je zadano vertikalno opterećenje i $H$ intenzitet horizontalne komponente vlačne sile u užetu; povećanjem intenziteta sile u užetu, a time i intenziteta $H$ , smanjuje se provjes užeta. (Tu ćete diferencijalnu jednadžbu izvesti sljedeći semestar, u Mehanici 1.)

Viseći most

Na glavne nosive kabele mosta, razapete preko rijeke, obješena je s pomoću niza jednako razmaknutih vertikalnih kabela vodoravna kolnička konstrukcija. Iako su vertikalni kabeli za nosive kabele spojeni u diskretnim točkama, može se za preliminarni proračun uzeti da su spojevi „razmazani” uzduž nosivih kabela, tako da je i prijenos težine kolničke konstrukcije na nosive kabele „razmazan”. Iako u stvarnosti kabeli nisu bez težine, ona je obično zanemariva u odnosu na težinu kolničke konstrukcije. Ako je ta konstrukcija uzduž cijeloga raspona mosta jednakih poprečnih presjeka, opterećenje će biti jednoliko raspodijeljeno po horizontali, $q(x) = q_0$ , pa je diferencijalna jednadžba ravnoteže

$z''(x) = -\!\dfrac{q_0}{H}$ .

var ('q0 H')
var ('x_l z_l x_r z_r')
z = function ('z')(x)

deq = diff (z, x, 2) == -q0/H

zz(x) = desolve (deq, z, ivar = x)
zz

$\newcommand{\Bold}[1]{\mathbf{#1}}x \ {\mapsto}\ K_{2} x - \frac{q_{0} x^{2}}{2 \, H} + K_{1}$

Uvođenje rubnih uvjeta $z(x_l) = z_l$ i $z(x_r) = z_r$ :

zzbc(x) = desolve (deq, z, ivar = x, ics = [x_l, z_l, x_r, z_r])
zzbc

$\newcommand{\Bold}[1]{\mathbf{#1}}x \ {\mapsto}\ -\frac{q_{0} x^{2}}{2 \, H} + \frac{{\left(q_{0} x_{l}^{2} - q_{0} x_{r}^{2} + 2 \, H z_{l} - 2 \, H z_{r}\right)} x}{2 \, {\left(H x_{l} - H x_{r}\right)}} - \frac{q_{0} x_{l}^{2} x_{r} + 2 \, H x_{r} z_{l} - {\left(q_{0} x_{r}^{2} + 2 \, H z_{r}\right)} x_{l}}{2 \, {\left(H x_{l} - H x_{r}\right)}}$

Rubni uvjeti $z(-1) = -1$ i $z(1) = -1$ ; različiti intenziteti sile $H$ :

zz0 = zzbc.subs (q0 = 3, H = 1, x_l = -1, z_l = -1, x_r = 1, z_r = -1)
zz0

$\newcommand{\Bold}[1]{\mathbf{#1}}x \ {\mapsto}\ -\frac{3}{2} \, x^{2} + \frac{1}{2}$

zz1 = zzbc.subs (q0 = 3, H = 2, x_l = -1, z_l = -1, x_r = 1, z_r = -1)
zz1

$\newcommand{\Bold}[1]{\mathbf{#1}}x \ {\mapsto}\ -\frac{3}{4} \, x^{2} - \frac{1}{4}$

zz2 = zzbc.subs (q0 = 3, H = 5, x_l = -1, z_l = -1, x_r = 1, z_r = -1)
zz2

$\newcommand{\Bold}[1]{\mathbf{#1}}x \ {\mapsto}\ -\frac{3}{10} \, x^{2} - \frac{7}{10}$

(plot (zz0, (x, -1, 1)) + plot (zz1, (x, -1, 1), color = 'red') + plot (zz2, (x, -1, 1), color = 'green')) . show (axes_labels = ['x', 'z'], ymin = 0.5, ymax = -1, figsize = 6)

Rubni uvjeti $z(0) = 0$ i $z(2,5) = -1$ ; različiti intenziteti sile $H$ :

zz3 = zzbc.subs (q0 = 3, H = 1, x_l = 0, z_l = 0, x_r = 5/2, z_r = -1)
zz3

$\newcommand{\Bold}[1]{\mathbf{#1}}x \ {\mapsto}\ -\frac{3}{2} \, x^{2} + \frac{67}{20} \, x$

zz4 = zzbc.subs (q0 = 3, H = 2, x_l = 0, z_l = 0, x_r = 5/2, z_r = -1)
zz4

$\newcommand{\Bold}[1]{\mathbf{#1}}x \ {\mapsto}\ -\frac{3}{4} \, x^{2} + \frac{59}{40} \, x$

zz5 = zzbc.subs (q0 = 3, H = 5, x_l = 0, z_l = 0, x_r = 5/2, z_r = -1)
zz5

$\newcommand{\Bold}[1]{\mathbf{#1}}x \ {\mapsto}\ -\frac{3}{10} \, x^{2} + \frac{7}{20} \, x$

(plot (zz3, (x, 0, 2.5)) + plot (zz4, (x, 0, 2.5), color = 'red') + plot (zz5, (x, 0, 2.5), color = 'green')) . show (axes_labels = ['x', 'z'], ymin = 1.9, ymax = -1, figsize = 6)

Teško uže ... ili lanac

Jedino je opterećenje homogenoga užeta konstantne debljine njegova težina. To je opterećenje jednoliko raspodijeljeno po duljini užeta: $q(x) = q_0 \sqrt{1 + \big(z'(x)\big)^2}$ . Diferencijalna je jednadžba ravnoteže sada

$z''(x) = -\!\dfrac{q_0}{H}\sqrt{1 + \big(z'(x)\big)^2}$ .

Krivulje koje su grafovi njezinih rješenja nazivaju se hiperboličnim lančanicama.

var ('q0 H')
var ('x_l z_l x_r z_r')
z = function ('z')(x)

deq = diff (z, x, 2) == -q0/H * sqrt (1 + diff (z, x)^2)

zz(x) = desolve (deq, z, ivar = x)
zz

$\newcommand{\Bold}[1]{\mathbf{#1}}x \ {\mapsto}\ K_{2} - \frac{H \cosh\left(\frac{K_{1} q_{0} + q_{0} x}{H}\right)}{q_{0}}$

Na žalost, u ovom slučaju SageMath ne zna uvrstiti rubne uvjete, primjerice $z(-1) = 0$ i $z(1) =0$ :

zzbc(x) = desolve (deq, z, ivar = x, ics = [-1, 0, 1, 0])
zzbc

$\newcommand{\Bold}[1]{\mathbf{#1}}x \ {\mapsto}\ \left(\right)$

Naime, SageMath ne zna riješiti sustav dviju nelinearnih jednadžbi s nepoznanicama $K_1$ i $K_2$ :

print zz

x |--> _K2 - H*cosh((_K1*q0 + q0*x)/H)/q0

x |--> _K2 - H*cosh((_K1*q0 + q0*x)/H)/q0

var ('_K1 _K2')
solve ([zz(-1) == 0, zz(1) == 0], [_K1, _K2], to_poly_solve = 'force')

$\newcommand{\Bold}[1]{\mathbf{#1}}\left[K_{2} - \frac{H \cosh\left(\frac{K_{1} q_{0} - q_{0}}{H}\right)}{q_{0}} = 0, K_{2} - \frac{H \cosh\left(\frac{K_{1} q_{0} + q_{0}}{H}\right)}{q_{0}} = 0\right]$

... čak ni ako uvrstimo vrijednosti za $q_0$ i $H$ :

zz0 = zz.subs(q0 = 1, H = 1.25)
solve ([zz0(-1) == 0, zz0(1) == 0], [_K1, _K2], to_poly_solve = 'force')

$\newcommand{\Bold}[1]{\mathbf{#1}}\left[K_{2} - 1.25 \, \cosh\left(0.8 \, K_{1} - 0.8\right) = 0, K_{2} - 1.25 \, \cosh\left(0.8 \, K_{1} + 0.8\right) = 0\right]$

Stoga ćemo sustav riješiti približno, „grafički”, očitavanjem vrijednosti s crteža:

implicit_plot (zz0(-1) == 0, (_K1, -5, 5), (_K2, -5, 5)) + implicit_plot (zz0(1) == 0, (_K1, -5, 5), (_K2, -5, 5), figsize = 6)

implicit_plot (zz0(-1) == 0, (_K1, -1, 1), (_K2, 0, 2)) + implicit_plot (zz0(1) == 0, (_K1, -1, 1), (_K2, 0, 2), figsize = 6)

implicit_plot (zz0(-1) == 0, (_K1, -0.05, 0.05), (_K2, 1.6, 1.7)) + implicit_plot (zz0(1) == 0, (_K1, -0.05, 0.05), (_K2, 1.6, 1.7))

... očitano: $K_1 = 0$ , $K_2 \approx 1,\!672$

N (zz0.subs(_K1 = 0, _K2 = 1.672)(-1))

$\newcommand{\Bold}[1]{\mathbf{#1}}0.000206317118944144$

N (zz0.subs(_K1 = 0, _K2 = 1.672)(1))

$\newcommand{\Bold}[1]{\mathbf{#1}}0.000206317118944144$

... pa je rješenje diferencijalne jednadžbe za $q_0 = 1$ i $H = 1,\!25$ , uz rubne uvjete $z(-1) = 0$ i $z(1) = 0$ :

zz00 = zz0.subs(_K1 = 0, _K2 = 1.672)
zz00

$\newcommand{\Bold}[1]{\mathbf{#1}}x \ {\mapsto}\ -1.25000000000000 \, \cosh\left(0.800000000000000 \, x\right) + 1.67200000000000$

plot (zz00, ymin = 0.5, ymax = 0, figsize = 6)

Na sljedećoj su slici—usporedbe radi—prikazani graf rješenja diferencijalne jednadžbe za $q_0 = 1$ i $H = 1,\!25$ i rubne uvjete $z(-1) = 1$ i $z(1) = 1$ (lančanica) i graf polinoma drugog stupnja koeficijenti kojega su odabrani tako da se njegove vrijednosti podudaraju s vrijednostima rješenja u $-1$ , $0$ i $1$ .

show (plot (zz00, legend_label = ' rjesenje dif. jedn.') + plot (-0.422 * x^2 + 0.422, color = 'red', legend_label = ' kvadratni polinom'), ymin = 0.5, ymax = 0, axes_labels = ['x', 'z'], figsize = 7)

Napomena: spomenuli smo na šestomu predavanju da se sustavi nelinearnih algebarskih jednadžbi koje SageMath ne zna riješiti mogu numerički rješavati primjenom funkcija modula optimize (Optimization and root finding) programskoga paketa SciPy, koji je uključen u SageMath.

MPZI_predavanje_08

2437 days ago by fresl