Mehanika_1-03_Ekvivalencija_(v0.9)

Funkcije koje smo definirali u radnim listovima Mehanika_1-01_Sila i Mehanika_1-02_Moment uvedene su u i ovaj radni list.

Mehanika 1.

Statička ekvivalencija

[Natuknice možete naći i u datoteci  Statička ekvivalencija  u  Bilješkama i skicama s predavanja iz Mehanike 1.]

Na prošlom smo predavanju uveli uvjete ravnoteže tijela na koje djeluju koncentrirane sile  $\big\{\vec{F}_i\big\}_{i = 0}^{n-1}$  i koncentrirani momenti  $\big\{\vec{M}_i\big\}_{j = 0}^{m-1}$:

1. iščezavanje zbroja svih sila:  

vektorski oblik:

$\displaystyle\sum_{i = 0}^{n-1} \vec{F}_i \:=\: \vec{0}$

skalarni oblik:

$\displaystyle\sum_{i = 0}^{n-1} F_{i,x} \:=\: 0$

$\displaystyle\sum_{i = 0}^{n-1} F_{i,y} \:=\: 0$

$\displaystyle\sum_{i = 0}^{n-1} F_{i,z} \:=\: 0$

2. iščezavanje zbroja momenata svih sila u odnosu na bilo koju točku (odabrali smo ishodište) i svih koncentriranih momenata:  

vektorski oblik:

$\displaystyle\sum_{i = 0}^{n-1} \vec{r}_{F_i/O}\times\vec{F}_i  \,+\, \displaystyle\sum_{j = 0}^{m} \vec{M}_j  \:=\: \vec{0}$

skalarni oblik:

$\displaystyle\sum_{i = 0}^{n-1} (y_i\,F_{i,z} - z_i\,F_{i,y}) \,+\, \displaystyle\sum_{j = 0}^{m-1} M_{j,x}  \:=\: 0$

$\displaystyle\sum_{i = 0}^{n-1} (-x_i\,F_{i,z} + z_i\,F_{i,x}) \,+\, \displaystyle\sum_{j = 0}^{m-1} M_{j,y}  \:=\: 0$

$\displaystyle\sum_{i = 0}^{n-1} (x_i\,F_{i,y} - y_i\,F_{i,x}) \,+\, \displaystyle\sum_{j = 0}^{m-1} M_{j,z}  \:=\: 0$

Dva su sistema sila i koncentriranih momenata statički ekvivalentna ako su njihovi doprinosi uvjetima ravnoteže jednaki.

Primjer 1.: 

Paralelni pomak sile ili redukcija sile na točku

Izračunat ćemo djelovanje sile  $\vec{F} = -4\,\vec{\imath} + 3\,\vec{\jmath} - 2\,\vec{k}$,  s hvatištem u ishodištu, na točku  $A = \big(\!\frac{5}{3}, \frac{7}{3}, 2\big)$.  (Točka $A$ ne leži na pravcu djelovanja sile $\vec{F}$.)

• u točki $A$ dodajemo sile  $\vec{F}$  i  $-\vec{F}\,$;  budući da te sile djeluju na istom pravcu i da je  $\vec{F} + (-\vec{F}\;) \,=\, \vec{F} - \vec{F} \,=\, \vec{0}$,  može se reći da nismo dodali ništa ...

• ... ali, sila $\vec{F}$  u točki $O$ i sila $-\vec{F}$  u točki $A$ tvore spreg ...

• ... moment kojega je  $\vec{M}_{\pm F} \,=\, \vec{r}_{\!O/A}\times \vec{F}$ ...

• ... sila $\vec{F}$ koja djeluje u točki $O$  (i, općenitije, na pravcu kroz točku $O$)  može se, prema tome, zamijeniti silom $\vec{F}$ u točki $A$  (općenitije: na pravcu kroz $A$)  i momentom sprega $\vec{M}_{\pm F}$  (koji obično crtamo u točki $A$, iako je, znamo, njegov položaj u prostoru neodređen) ...

• ... ali je, naravno,  $\vec{M}_{\pm F} \,\perp\, \vec{F}$.

Rezultirajuće djelovanje sistema sila  $\boldsymbol{\Big\{\vec{F}_i\Big\}_{i = 0}^{n-1}}$  i koncentriranih momenata  $\boldsymbol{\Big\{\vec{M}_i\Big\}_{j = 0}^{m-1}}$  u odnosu na točku $\boldsymbol{A}$  (ili dinama u točki $A$)

Svaki se sistem sila i koncentriranih momenata može na bezbrojno mnogo načina zamijeniti statički ekvivalentnim sistemom koji sadrži jednu silu i jedan moment; u posebnim slučajevima mogu iščeznuti ili sila ili moment ili i sila i moment. Samo jedno rješenje dobiva se odabere li se točka kojom zamjenjujuća sila prolazi i u odnosu na koju se izračunavaju momenti sila zadanoga sistema. 

U općem je slučaju sistem s jednom silom i jednim momentom najjednostavniji statički ekvivalentan sistem na koji se zadani sistem sila i momenata može svesti. Takav sistem nazivamo rezultirajućim djelovanjem u odnosu na odabranu točku $A$, silu koju sadrži rezultirajućom silom, a moment rezultirajućim momentom.

Rezultirajuća sila ili glavni vektor sila zbroj je svih sila zadanoga sistema:

$\vec{F}_{R/A} \:=\: \displaystyle\sum_{i=0}^{n-1} \vec{F}_i \:=\: \vec{F}_R$;

uzima se da je njezino hvatište točka $A$.

Rezultirajući moment u odnosu na točku $A$ ili glavni vektor momenata zbroj je momenata svih sila zadanoga sistema u odnosu na tu točku i svih zadanih koncentriranih momenata:

$\vec{M}_{R/A} \:=\: \displaystyle\sum_{i=0}^{n-1} \vec{r}_{F_i/A} \times \vec{F}_i \:+\, \displaystyle\sum_{j=0}^{m-1} \vec{M}_j$

Primjer 1.:  (nastavak)

Djelovanje sile $\vec{F}$ na točku $A$ izračunat ćemo sada prema definiciji rezultirajućega djelovanja:

• rezultirajuća sila:  $\vec{F}_{R/A} \,=\, \vec{F}_R \,=\, \vec{F}$
• rezultirajući moment:  $\vec{M}_{R/A} \,=\, \vec{r}_{F/A}\times\vec{F}$

• rezultirajuća sila:

• rezultirajući moment u odnosu na točku $A$:

• položajni vektor sile $\vec{F}$ u odnosu na točku $A$:

$\vec{r}_{F/A} \,=\, \vec{r}_{O/A}$

• moment sile $\vec{F}$ u odnosu na točku $A$:

• rezultirajuće djelovanje u odnosu na točku $A$:

Primjer 1.:  (još jedan nastavak, s važnim zaključkom)

Neka je $B$ točka na pravcu koji točkom $A$ prolazi paralelno s pravcem djelovanja sile $\vec{F}$, primjerice  $B = \big(\!-1, \frac{13}{3}, \frac{2}{3}\big)$. Izračunat ćemo djelovanje sile $\vec{F}$ (s hvatištem u ishodištu) na točku $B$. 

Zaključak:  djelovanje je sile $\vec{F}$ na sve točke pravca paralelnoga s pravcem njezina djelovanja jednako.

Primjer, naravno, nije dokaz, pa slijedi i formalni dokaz:

$\vec{M}_{F/B} \:=\: \vec{r}_{F/B} \times \vec{F} \:=\: (\vec{r}_{A/B} \,+\, \vec{r}_{F/A}) \times \vec{F} \:=\: \underbrace{\vec{r}_{A/B} \times \vec{F}}_{\displaystyle = \vec{0}} \,+\, \vec{r}_{F/A} \times \vec{F} \:=\: \vec{r}_{F/A} \times \vec{F} \:=\: \vec{M}_{F/A}$

[Zašto je  $\vec{r}_{A/B} \times \vec{F} \,=\, \vec{0}$?]

Primjer 2.:

Sila  $\vec{F}_0 \,=\, \frac{9}{5}\,\vec{\imath}$  djeluje u točki  $C_0 = \big(\frac{1}{4}, \frac{1}{4}, -\frac{5}{6}\big)$,  a sila  $\vec{F}_1 \,=\, \frac{13}{5}\,\vec{\jmath} + \frac{5}{7}\, \vec{k}$  u točki $C_1 = \big(\!-\!1, 0, \frac{7}{8}\big)$.  (Pravci djelovanja sila $\vec{F}_0$ i $\vec{F}_1$ su mimosmjerni. Točka $A$ leži na pravcu djelovanja sile $\vec{F}_0$.)  Zadan je i koncentrirani moment  $\vec{M}_0 = -\frac{7}{4}\,\vec{\imath} + \frac{17}{5}\,\vec{\jmath} + \frac{3}{4}\,\vec{k}$.

Izračunat ćemo rezultirajuće djelovanje sistema  $\big\{\vec{F}_0, \vec{F}_1, \vec{M}_0 \big\}$  u odnosu na točku  $A = \big(\!-\!\frac{1}{2}, \frac{1}{4}, -\frac{5}{6}\big)$.

•  zadane sile, moment i točka $A$:

• koncentrirani moment $\vec{M}_0$ možemo staviti u bilo koju točku — stavit ćemo ga u točku $A$:

• rezultirajuća sila u točki $A$:

$\vec{F}_{R/A} \:=\: \vec{F}_R \:=\: \displaystyle\sum_{i=0}^{n-1} \vec{F}_i \:=\: \vec{F}_0 \,+\, \vec{F}_1$

• položajni vektori sila u odnosu na točku $A$:

$\vec{r}_{F_0/A} = \vec{r}_{C_0/A}$   i   $\vec{r}_{F_1/A} = \vec{r}_{C_1/A}$

• moment sile $\vec{F}_0$ u odnosu na točku $A$:

$\vec{M}_{F_0/A} = \vec{0}$      [zašto?]

• moment sile $\vec{F}_1$ u odnosu na točku $A$:

$\vec{M}_{F_1/A} \,=\, \vec{r}_{F_1/A}\times \vec{F}_1$

• rezultirajući moment u odnosu na točku $A$:

$\vec{M}_{R/A} \:=\: \displaystyle\sum_{i=0}^{n-1} \vec{M}_{F_i/A} \:+\, \displaystyle\sum_{j=0}^{m-1} \vec{M}_j \:=\: \vec{M}_{F_0/A} \,+\, \vec{M}_{F_1/A} \,+\, \vec{M}_0$

• rezultirajuće djelovanje u odnosu na točku $A$:

Rezultirajuću silu i rezultirajući moment možemo i „grafički” konstruirati:

• djelovanje u točki $A$ statički ekvivalentno zadanim silama — sile $\vec{F}_0$ i $\vec{F}_1$ paralelno su pomaknute u točku $A$ dodavanjem momenta $\vec{M}_{F_1/A}$:

• rezultirajuća sila u točki $A$,  $\vec{F}_{R/A} \:=\: \vec{F}_0 \,+\, \vec{F}_1$,  dobivena s pomoću paralelograma sila, ...

• ... i rezultirajući moment u odnosu na točku $A$,  $\vec{M}_{R/A} \:=\: \vec{M}_{F_1/A} \,+\, \vec{M}_0$ ...

• ... zajedno tvore rezultirajuće djelovanje u odnosu na točku $A$:

Iako i rezultirajuću silu i rezultirajući moment prikazujemo vektorima, ta dva vektora ne možemo zbrojiti.

Rezultirajuće djelovanje u odnosu na (neku drugu) točku $\boldsymbol{B}$

Ako je poznato rezultirajuće djelovanje sistema sila i momenata u odnosu na točku $A$, onda se rezultirajuće djelovanje u odnosu na točki $B$ može izračunati prema sljedećim izrazima:

• rezultirajuća sila:   

$\vec{F}_{R/B} \:=\: \vec{F}_{R/A}$, 

• rezultirajući moment:  

$\vec{M}_{R/B} \:=\; \vec{r}_{A/B} \times \vec{F}_R \:+\: \vec{M}_{R/A}$.

Izraz za rezultirajuću silu slijedi neposredno iz njezine definicije,

$\vec{F}_{R/B} \:=\: \displaystyle\sum_{i=0}^{n-1} \vec{F}_i \:=\: \vec{F}_R \:=\: \vec{F}_{R/A}$,

dok je izvod izraza za rezultirajući moment nešto složeniji.  Provest ćemo ga uz primjer (ali će svi izrazi u izvodu biti opći).

Primjer 2. (nastavak):

Izračunat ćemo rezultirajuće djelovanje sistema  $\big\{\vec{F}_0, \vec{F}_1, \vec{M}_0\big\}$  u odnosu na točku  $B = \big(\!-\!\frac{2}{5}, \frac{69}{43}, 0\big)$.

•  rezultirajuća sila (u odnosu na točku $B$): 

$\vec{F}_{R/B} \,=\, \vec{F}_R \,=\, \displaystyle\sum_{i=0}^{n-1} \vec{F}_i \,=\, \vec{F}_0 + \vec{F}_1$

I u izvodu izraza za rezultirajući moment u odnosu na točku $B$ polazimo od njegove definicije:

$\vec{M}_{R/B} \:=\: \displaystyle\sum_{i=0}^{n-1} \vec{r}_{F_i/B} \times \vec{F}_i \:+\, \displaystyle\sum_{j=0}^{m-1} \vec{M}_j$.

•  položajni vektori sila u odnosu na točku $B$:

Položajni vektor $\vec{r}_{F_i/B}$ sile $\vec{F}_i$ u odnosu na točku $B$ možemo izraziti kao zbroj položajnoga vektora $\vec{r}_{A/B}$ točke $A$ u odnosu na točku $B$ i položajnoga vektora $\vec{r}_{F_i/A}$ sile $\vec{F}_i$ u odnosu na točku $A$,  $\vec{r}_{F_i/B} = \vec{r}_{A/B} + \vec{r}_{F_i/A}$.

•  položajni vektor $\vec{r}_{A/B}$:

•  $\vec{r}_{F_i/B} = \vec{r}_{A/B} + \vec{r}_{F_i/A}$:

Izraz za rezultirajući moment u odnosu na točku $B$ sada je

$\vec{M}_{R/B} \:=\: \displaystyle\sum_{i=0}^{n-1} \big(\vec{r}_{A/B} +  \vec{r}_{F_i/A}\big) \times \vec{F}_i \:+\, \displaystyle\sum_{j=0}^{m-1} \vec{M}_j$.

Primjena zakona distributivnosti za vektorski produkt u prvome pribrojniku daje

$\vec{M}_{R/B} \:=\: \displaystyle\sum_{i=0}^{n-1} \vec{r}_{A/B} \times \vec{F}_i \:+\, \displaystyle\sum_{i=0}^{n-1} \vec{r}_{F_i/A} \times \vec{F}_i \:+\, \displaystyle\sum_{j=0}^{m-1} \vec{M}_j$.

Uz još jednu je primjenu zakona distributivnosti u novodobivenu prvom pribrojniku

$\vec{M}_{R/B} \:=\; \vec{r}_{A/B}\times \underbrace{\displaystyle\sum_{i=0}^{n-1} \vec{F}_i}_{\textstyle \vec{F}_R} \;+\, \underbrace{\,\displaystyle\sum_{i=0}^{n-1} \vec{r}_{F_i/A} \times \vec{F}_i \:+\, \displaystyle\sum_{j=0}^{m-1} \vec{M}_j\,}_{\textstyle \vec{M}_{R/A}}$.

• rezultirajuće djelovanje u odnosu na točku $A$:

Konačni je izraz za rezultirajući moment u odnosu na točku $B$:

$\vec{M}_{R/B} \:=\; \vec{r}_{A/B} \times \vec{F}_R \:+\: \vec{M}_{R/A}$.

•  statički ekvivalentno djelovanje u točki $B$  $\big(\vec{F}_R$,  $\vec{r}_{A/B} \times \vec{F}_R$  i  $\vec{M}_{R/A}\big)$:

•  rezultirajuće djelovanje u odnosu na točku $B$  $\big(\vec{F}_R$  i  $\vec{M}_{R/B}\big)$:

Rezultirajuće djelovanja u točki $B$ izračunat ćemo i neposredno (prema definiciji):

• rezultirajuća sila: 

$\vec{F}_{R/B} \,=\, \vec{F}_R \,=\, \displaystyle\sum_{i=0}^{n-1} \vec{F}_i \,=\, \vec{F}_0 + \vec{F}_1$

• rezultirajući moment u odnosu na točku $B$:

$\vec{M}_{R/B} \:=\: \displaystyle\sum_{i=0}^{n-1} \vec{M}_{F_i/B} \:+\, \displaystyle\sum_{j=0}^{m-1} \vec{M}_j \:=\: \vec{M}_{F_0/B} \,+\, \vec{M}_{F_1/B} \,+\, \vec{M}_0$

• položajni vektori sila u odnosu na točku $B$ ...

• ... i „pomak” momenta $\vec{M}_0$ u točku $B$:

• momenti sila u odnosu na točku $B$:

• rezultirajući moment:

• rezultirajuće djelovanje u odnosu na točku $B$:

• „grafička” konstrukcija rezultirajućega djelovanja:

• uvođenje momenata sila u odnosu na točku $B$ omogućava paralelni pomak sila u nju ...

• ... i „grafičke” konstrukcije rezultirajuće sile (paralelogram sila) i rezultirajućega momenta (paralelepiped momenata):

Iz zaključka još jednoga nastavka primjera 1. slijedi da je rezultirajuće djelovanje na sve točke pravca paralelnoga s pravcem djelovanja rezultirajuće sile jednako.

Invarijante sistema sila i koncentriranih momenata

Invarijanta je matematička ili fizička karakteristika nekog matematičkog pojma ili fizičke pojave, čija veličina ne ovisi o izboru koordinatnoga ili, općenitije, referentnog sustava u kojemu je određena.

Invarijante sistema sila i koncentriranih momenata veličine su koje ne ovise o izboru točke u odnosu na koju je izračunano njegovo rezultirajuće djelovanje.

Prva je invarijanta rezultirajuća sila sistema:

$\vec{F}_R \:=\: \displaystyle\sum_{i=0}^{n-1} \vec{F}_i \:=\: \vec{F}_{R/A} \:=\: \vec{F}_{R/B} \:=\: \ldots$

Neka je $\vec{M}_{R/T}$ rezultirajući moment sistema u odnosu na neku, bilo koju točku $T$.  Druga je invarijanta ortogonalna projekcija $\vec{M}_R$ momenta $\vec{M}_{R/T}$ na bilo koju os $o$ paralelnu s pravcem djelovanja sile $\vec{F}_R$:

$\vec{M}_R \:=\: \big(\vec{M}_{R/T}\cdot\vec{e}_o\big)\,\vec{e}_o \:=\: \big(\vec{M}_{R/A}\cdot\vec{e}_o\big)\,\vec{e}_o \:=\: \big(\vec{M}_{R/B}\cdot\vec{e}_o\big)\,\vec{e}_o \:=\: \ldots, \qquad  \vec{e}_o \,=\, \vec{e}_R \,=\, \dfrac{\vec{F}_R}{\big\|\vec{F}_R\big\|}$.

Dokaz invarijantnosti vektora $\vec{M}_R$ neposredno slijedi iz ranije izvedenoga izraza

$\vec{M}_{R/B} \:=\: \vec{r}_{A/B}\times\vec{F}_R  \,+\, \vec{M}_{R/A}$  

i činjenice da su vektori  $\vec{r}_{A/B}\times\vec{F}_R$  i  $\vec{F}_R$  međusobno okomiti (ako  $\vec{r}_{A/B}\times\vec{F}_R \ne \vec{0}$):  vektori $\vec{M}_{R/A}$ i $\vec{M}_{R/B}$ za bilo koje dvije točke $A$ i $B$ razlikuju se stoga za vektor koji je okomit na pravac djelovanja sile $\vec{F}_R$, pa njegova ortogonalna projekcija na os paralelnu s tim pravcem iščezava.

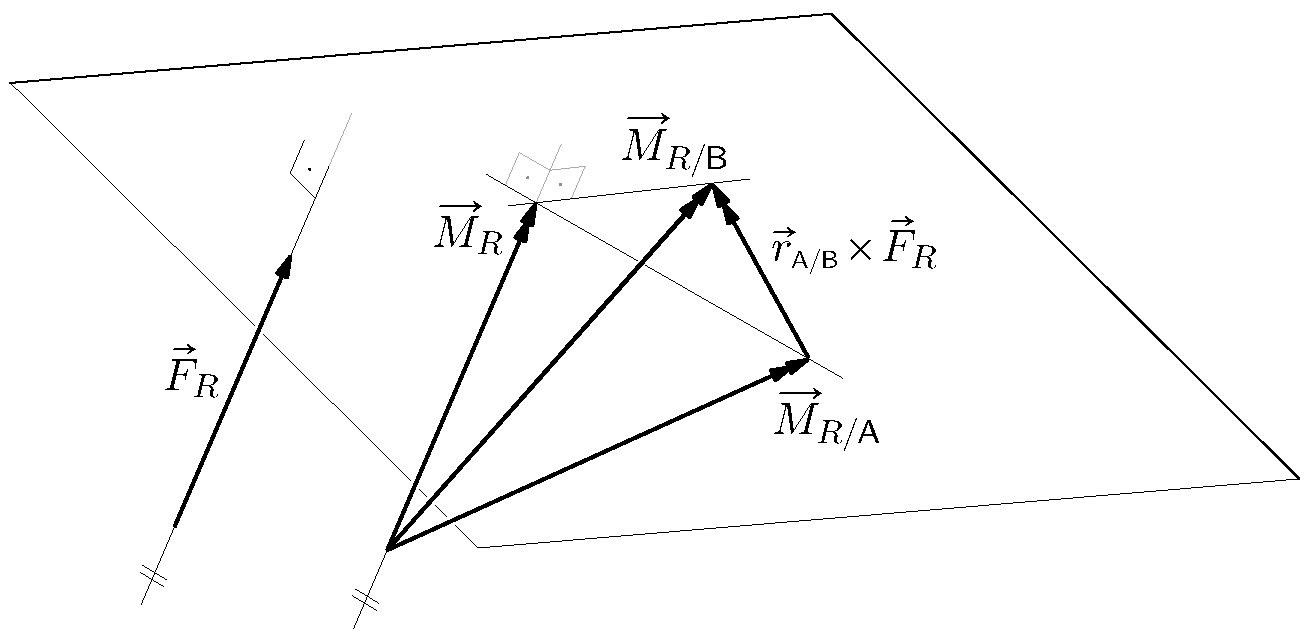
Lako je vidjeti da je $\vec{M}_{R}$  rezultirajući moment najmanjega intenziteta koji se može pojaviti. 

Primjer 2.  (još jedan nastavak):

Provjerit ćemo je li  $\big(\vec{M}_{R/A}\cdot\vec{e}_R\big)\,\vec{e}_R \:=\: \big(\vec{M}_{R/B}\cdot\vec{e}_R\big)\,\vec{e}_R$.

U stvari, dovoljno je provjeriti jesu li vrijednosti projekcija jednake — je li  $\vec{M}_{R/A}\cdot\vec{e}_R \:=\: \vec{M}_{R/B}\cdot\vec{e}_R$.

Centralna os $\mathit\&$ dinamički vijak

Centralna os je pravac za sve točke $C_\xi$ kojega vrijedi da su pripadni rezultirajući momenti $\vec{M}_{R/C_\xi}$ paralelni s rezultirajućom silom $\vec{F}_R$.  Centralna os postoji samo ako je  $\vec{F}_R \ne \vec{0}$.

Centralna je os paralelna s pravcem djelovanja rezultirajuće sile $\vec{F}_R$  [dokažite!]. 

Neka je $\vec{M}_{R/T}$ rezultirajući moment sistema u odnosu na bilo koju točku $T$ i neka je $\vec{M}_R$ je ortogonalna projekcija momenta $\vec{M}_{R/T}$ na bilo koju os $o$ paralelnu s pravcem djelovanja sile $\vec{F}_R$,

$\vec{M}_R \:=\: \big(\vec{M}_{R/T}\cdot\vec{e}_R\big)\,\vec{e}_R.$

Dokažite da su svi $\vec{M}_{R/C_\xi}$ jednaki $\vec{M}_{R}$!

Ako se centralna os uzme za pravac djelovanja sile $\vec{F}_R$, rezultirajuće se djelovanje naziva dinamičkim vijkom.

Polje rezultirajućih djelovanja u točkama ravnine okomite na centralnu os:

Prostorno polje rezultirajućih momenata:

Opis općega linearnoalgebarskog postupka određivanja položaja centralne možete naći u udžbeniku Heinricha Wernera Mehanika I. Statika, a osnovne izraze i u datoteci Statička ekvivalencija. Ovdje ćemo prikazati tek dva jednostavnija primjera.

Primjer 3.:

Sila  $\vec{F}_0 = \vec{\jmath}$  djeluje u ishodištu, a sila  $\vec{F}_1 = \vec{\imath}$  u točki  $A = (0, 0, 1)$.  Odredit ćemo pripadni dinamički vijak.

• u ishodištu dodajemo sile  $\vec{F}_1$  i  $-\vec{F}_1$ ...

• ... rezultirajuća sila je  $\vec{F}_R = \vec{F}_0 + \vec{F}_1$;   sile $\vec{F}_0$ i $\vec{F}_1$, koje djeluju u ishodištu, možemo zamijeniti silom $\vec{F}_R$, također u ishodištu ...

• ... sile  $\vec{F}_1$  u $A$ i  $-\vec{F}_1$  u ishodištu tvore spreg koji zamjenjujemo momentom sprega $\vec{M}_1$ ...

• ... moment $\vec{M}_1$ rastavljemo u komponente $\vec{M}{}_1^{\,\|}$ i $\vec{M}{}_1^{\perp}$:  $\vec{M}_1 = \vec{M}{}_1^{\,\|} + \vec{M}{}_1^{\perp}$;   komponenta $\vec{M}{}_1^{\,\|}$ paralelna je s pravcem djelovanja sile $\vec{F}_R$, pa je možemo izračunati kao ortogonalnu projekciju na taj pravac (komponenta $\vec{M}{}_1^{\,\|}$ druga je invarijanta $\vec{M}_R$ sistema $\big\{ \vec{F}_0, \vec{F}_1 \big\}$) ...

• ... komponenta $\vec{M}{}_1^{\perp}$ okomita je na pravac djelovanja sile $\vec{F}_R$, a izračunati je možemo prema izrazu  $\vec{M}{}_1^{\perp} = \vec{M}_1 - \vec{M}{}_1^{\,\|}$ ...

• ... moment  $\vec{M}{}_1^{\perp}$  ćemo zamijeniti spregom sila  $\vec{F}_R$  i  $-\vec{F}_R$;  sila  $-\vec{F}_R$  djelovat će u ishodištu, a hvatište sile  $\vec{F}_R$  (općenitije, pravac njezina djelovanja) odredit ćemo iz uvjeta da je moment sprega jednak momentu  $\vec{M}{}_1^{\perp}$:

izraze  

$\vec{r}_{X/O}\times\vec{F}_R  = \vec{M}{}_1^{\perp}$     ili     $\vec{r}_{X/O}\times\vec{F}_R  - \vec{M}{}_1^{\perp} = \vec{0}$  

možemo smatriti sustavom koji sadrži tri jednadžbe s tri nepoznanice — komponente vektora $\vec{r}_{X/O}$, odnosno, koordinate tražene točke ...

• ... budući da rješenje sadrži neodređeni koeficijent $r_I$, postoji $\infty^1$ rješenja — riječ je točkama na pravcu  [kojemu?];  za hvatište sile $\vec{F}_R$ možemo uzeti bilo koju njegovu točku ...

•  ... za sile  $\vec{F}_R$  i  $-\vec{F}_R$  koje djeluju u ishodištu je  $\vec{F}_R + (-\vec{F}_R) = \vec{F}_R - \vec{F}_R = \vec{0}$,  pa preostaju samo sila  $\vec{F}_R$  u točki $B$ i moment  $\vec{M}{}_1^{\,\|} = \vec{M}_R$ ...

• ... pravac djelovanja sile $\vec{F}_R$ je centralna os, a sila $\vec{F}_R$ i moment $\vec{M}_R$  čine dinamički vijak  ...

Pogodno je uzeti da je uz rezultirajuću silu $\vec{F}_{R}$ na centralnoj osi i rezultirajući moment $\vec{M}_{R}$.

Primjer 4.:

Sila  $\vec{F}_0 = \vec{\imath}$  djeluje u točki  $A_0 = \big(\!\frac{5}{4}, 0, 0\big)$,  $\vec{F}_1 = 2\,\vec{\jmath}$  u točki  $A_1 = \big(0, \frac{9}{4}, 0\big)$,  a sila  $\vec{F}_2 = 2\,\vec{k}$  u točki  $A_2 = \big(\!\frac{9}{8}, \frac{9}{4}, 0\big)$.  Odredit ćemo njihov dinamički vijak.  [Priču koja prati/opisuje slike ispričajte sami!]

Rezultanta

Ako rezultirajući moment dinamičkoga vijka iščezava, rezultirajuća se sila naziva rezultantom.  Rezultanta je, dakle, sila koja je sama statički ekvivalentna zadanom sistemu sila i koncentriranih momenata.

Pravac djelovanja rezultante je centralna os.

U primjeru 4.  je  $\vec{M}_{R} = \vec{M}{}^{\|}_{R/O} = \vec{0}$.  Slijedi da je  $\vec{M}_{R/O} = \vec{M}{}^\perp_{R/O}$,  a to znači da je  $\vec{M}_{R/O} \,\perp\, \vec{F}_R$.

Rezultanta, prema tome, postoji ako je  $\vec{M}_{R/T} \perp \vec{F}_R$  za neku točku $T$ izvan centralne osi. 

Polje rezultirajućih djelovanja u točkama ravnine okomite na centralnu os ako je  $\vec{M}_{R} = \vec{0}$:

Primjer 4.  (nastavak):

Drugi način određivanja rezultante — bez uvođenja rezultirajućega momenta.  [I sada opis slika možete ispričati sami.]