[Napomene o programskom kôdu u Sage-u:
Tekst poput ovoga, pisan slovima sans serif (bez vitica), odnosi se ponajprije na programski kôd.
Ćelije u kojima je prvi redak %auto ne trebate izvoditi ( evaluate ); one se izvode „same” pri otvaranju radnoga lista.
Funkcije, programska realizacija kojih nije bitna za razumijevanje gradiva Mehanike 1., „skrivene” su, a opisan je samo način njihova pozivanja.]
|
|
Funkcije koje smo definirali u radnom listu Mehanika_1-01_Sila uvedene su u i ovaj radni list (naredbom load (DATA + 'force.sage')).
Mehanika 1.
Pojam momenta
[Natuknice možete naći i u datoteci Pojam momenta u Bilješkama i skicama s predavanja iz Mehanike 1.]
Iščezavanje zbroja sila nuždan je i dovoljan uvjet za ravnotežu materijalne točke na koju te sile djeluju. Za ravnotežu tijela, ako sile imaju različita hvatišta i različite pravce djelovanja koji se ne sijeku u jednoj točki, to je tek nuždan, ali ne i dovoljan uvjet. (Poligon sila možemo oblikovati i ako sile koje zbrajamo nemaju isto hvatište.) Primjerice, djeluju li na tijelo dvije sile na usporednim pravcima, jednakih intenziteta, ali suprotnih orijentacija, tijelo će se (za)vrtjeti, iako zbroj sila iščezava. U obzir stoga treba uzeti i međusobni prostorni odnos sila koje djeluju na tijelo. Fizikalne veličine kojima se izražava utjecaj položajâ sila na uvjete ravnoteže (i, u kinetici, na zakone gibanja) nazivaju se momentima sila. Možemo parafrazirati Lagrangeovu „definiciju” sile (navedenu na prošlom predavanju): pod momentom sile razumije su općenito uzrok, bez obzira na njegovu vrstu, koji priopćava ili teži priopćiti vrtnju tijelima na koja djeluje; u stanju ravnoteže moment sile nema stvaran učinak, nego samo namiče težnju vrtnji, ali se može mjeriti učinkom koji bi stvorio da nije zapriječen.
Momentni je uvjet ravnoteže izveden iz brojnih pokusa s polugama (često tek misaonih), započetih u Arhimedovoj raspravi O ravnoteži likova ili o težištima likova i nastavljenih kroz skolastičko razdoblje do radova Simova Stevina; sarkastična ilustracija zakona poluge — španjolski plaćenik u Nizozemskoj — iz Stevinova je djela Provedba umijeća vaganja (1586.).

Položajni vektor
Položajni vektor ili radijus–vektor $\boldsymbol{\vec{r}_{\kern-0.2ex A}}$ točke $\boldsymbol{A}$ vektor je s početkom u ishodištu i vrhom u točki $A$: Ako je $A = (x_A, y_A, z_A)$, onda je
$\vec{r}_A \:=\: x_A\,\vec{\imath} \,+\, y_A\,\vec{\jmath} \,+\, z_A\,\vec{k}.$
Položajni vektor $\boldsymbol{\vec{r}_{\kern-0.2ex B/\kern-0.2ex A}}$ točke $\boldsymbol{B}$ u odnosu na točku $\boldsymbol{A}\,$ vektor je s početkom u točki $A$ i vrhom u točki $B$. Ako su $\vec{r}_{\!A}$ i $\vec{r}_B$ radijus–vektori točaka $A$ i $B$, onda je
$\vec{r}_{B/A} \:=\: \vec{r}_{B} - \vec{r}_{\!A} \:=\: (x_B - x_A)\,\vec{\imath} \,+\, (y_B - y_A)\,\vec{\jmath} \,+\, (z_B - z_A)\,\vec{k}.$
Primjer 1.:
Zadane su točke $A = (2, 3, 2)$ , $B = (-1, 2, -1)$ i $C = (-4, 1, -3)$. Izračunat ćemo i nacrtati položajni vektor točke $B$ u odnosu na točku $A$ i položajni vektor točke $C$ u odnosu na točku $B$.
- $\vec{r}_{B/A}$ — položajni vektor točke $B$ u odnosu na točku $A$:
(-3, -1, -2) (-3, -1, -2) |
|
|
- za grafički prikaz položajnoga vektora upotrebljavamo funkciju:
pv_arrow (v, tail = (0, 0, 0), color = 'green', thickness = 0.725)
- v — vektor
- tail — početak vektora
- $\vec{r}_{C/B}$ — položajni vektor točke $C$ u odnosu na točku $B$:
(-3, -1, -2) (-3, -1, -2) |
|
|
- na istoj slici, a dodat ćemo, usporedbe radi, i točku $D = (-3, -1, -2)$ i njezin radijus–vektor:
|
|
|
|
Položajni vektor $\boldsymbol{\vec{r}_{\kern-0.2ex F/\kern-0.2ex A}}$ pravca djelovanja sile $\boldsymbol{\vec{F}}$ u odnosu na točku $\boldsymbol{A}\,$ vektor je s početkom u točki $A$, dok mu je vrh u bilo kojoj točki pravca djelovanja sile $\vec{F}$. Položajni vektor pravca djelovanja sile često ćemo sažetije nazivati položajnim vektorom sile.
|
|
„Simbolički” položajni vektori:
position_vector_symb (a, b = None)
-
- a — oznaka točke ili sile položajni vektor koje se oblikuje
- b — oznaka točke u odnosu na koju se vektor oblikuje; ako se ne navede, podrazumijeva se ishodište
|
|
|
|
|
|
|
|
Moment sile (u odnosu) na točku
Moment sile $\boldsymbol{\vec{F}}$ u odnosu na točku $\boldsymbol{A}$ je vektor dobiven kao vektorski umnožak položajnoga vektora $\vec{r}_{F/A}$ i vektora sile $\vec{F}$,
$\vec{M}_{F/A} \;=\; \vec{r}_{F/A} \times \vec{F} \,\;=\; \left|\begin{array}{ccc} \vec{\imath} & \vec{\jmath} & \vec{k} \\ x_{F/A} & y_{F/A} & z_{F/A} \\ F_x & F_y & F_z \end{array}\right|$
$\phantom{\vec{M}_{F/A}} \;=\; \vec{\imath}\; \left|\begin{array}{cc} y_{F/A} & z_{F/A} \\ F_y & F_z \end{array}\right| \:-\: \vec{\jmath}\; \left|\begin{array}{cc} x_{F/A} & z_{F/A} \\ F_x & F_z \end{array}\right| \:+\: \vec{k}\; \left|\begin{array}{cc} x_{F/A} & y_{F/A} \\ F_x & F_y \end{array}\right| = $
$\phantom{\vec{M}_{F/A}} \;=\; (y_{F/A}\,F_z \,-\, z_{F/A}\,F_y)\:\vec{\imath} \:-\: (x_{F/A}\,F_z \,-\, z_{F/A}\,F_x)\:\vec{\jmath} \:+\: (x_{F/A}\,F_y \,-\,y_{F/A}\,F_x)\:\vec{k}$
|
|
|
|
- skalarne i vektorske komponente:
|
|
|
|
|
|
- vektor $\vec{r}_{F/A}$ obično se izražava pomoću neke točke $B$ na pravcu djelovanja sile $\vec{F}$: $\vec{r}_{F/A} = \vec{r}_{B/A} = \vec{r}_B - \vec{r}_A$
|
|
Prisjetite se: vektorski umnožak nije komutativan: $\vec{r}_{F/A} \times \vec{F} \;\:\ne\; \vec{F} \times \vec{r}_{F/A}$
False False |
... nego antikomutativan: $\vec{r}_{F/A} \times \vec{F} \;\:=\; -\vec{F} \times \vec{r}_{F/A}$
True True |
(ali je izraz $\vec{F} \times \vec{r}_{F/A}$ s mehaničkoga stajališta besmislen)
Vektor momenta označava se ponajčešće dvostrukom strelicom.
Za grafički prikaz vektora momenta upotrebljavat ćemo funkciju
m_arrow (mm, tail = (0, 0, 0), scale = 1, color = 'purple', thickness = 1)
- mm — vektor momenta
- tail — točka u kojoj djeluje vektor momenta
- množenjem vrijednošću scale može se promijeniti duljina prikaza vektora momenta
Primjer 2.:
Sila $\vec{F}_{\!A} = 3\,\vec{\imath} - 4\,\vec{\jmath} + \frac{1}{2} \vec{k}$ djeluje u točki $A = \big(\!\frac{3}{2}, \frac{7}{3}, 1\!\big)$, a sila $\vec{F}_O = \vec{F}_{\!A}$ u ishodištu. Izračunat ćemo moment sile $\vec{F}_{\!A}$ u odnosu na ishodište i moment sile $\vec{F}_O$ u odnosu na točku $A$.
Moment sile $\vec{F}_{\!A}$ u odnosu na ishodište
- sila $\vec{F}_{\!A}$ s hvatištem u točki $A$ i ishodište:
|
|
|
|
- položajni vektor $\vec{r}_{\!A/O}$:
(3/2, 7/3, 1) (3/2, 7/3, 1) |
|
|
- moment sile $\vec{F}_{\!A}$ u odnosu na ishodište:
$\vec{M}_{F_A/O} \,=\, \vec{r}_{\!A/O} \times \vec{F}_{\!A}$
(31/6, 9/4, -13) (31/6, 9/4, -13) |
|
|
- promjena mjerilâ sile i momenta:
|
|
Moment sile $\vec{F}_O$ u odnosu na točku $A$
- sila $\vec{F}_O = \vec{F}_A$ u ishodištu i točka $A$:
|
|
|
|
- položajni vektor $\vec{r}_{O/A}$:
(-3/2, -7/3, -1) (3/2, 7/3, 1) (-3/2, -7/3, -1) (3/2, 7/3, 1) |
|
|
- moment sile $\vec{F}_O$ u odnosu na točku $A$:
$\vec{M}_{F_O/A} \,=\, \vec{r}_{O/A} \times \vec{F}_O$
(-31/6, -9/4, 13) (-31/6, -9/4, 13) |
|
|
|
|
|
|
Funkcija za izračunavanje momenta sile $\vec{F}$ s hvatištem u točki $P$ u odnosu na točku $A$:
|
|
(31/6, 9/4, -13) (31/6, 9/4, -13) |
(-31/6, -9/4, 13) (-31/6, -9/4, 13) |
Svojstva momenta sile u odnosu na točku
(1) Za $\vec{F}\ne\vec{0}$ je $\vec{M}_{F/A}=\,\vec{0}$ ako je $\vec{r}_{F/A}=\vec{0}$ ili ako su $\vec{F}$ i $\vec{r}_{F/A}$ kolinearni. Drugim riječima, $\vec{M}_{F/A}=\,\vec{0}$ ako i samo ako pravac djelovanja sile $\vec{F}$ prolazi točkom $A$.
- $\vec{r}_{F/A}=\vec{0}$:
(0, 0, 0) (0, 0, 0) |
- ako su $\vec{F}$ i $\vec{r}_{F/A}$ kolinearni, onda je $\vec{r}_{F/A} = c\,\vec{F}$ za neki $c \ne 0$:
(0, 0, 0) (0, 0, 0) |
(2) Vektor $\vec{M}_{F/A}$ okomit je na ravninu koju razapinju vektori $\vec{F}$ i $\vec{r}_{F/A}$:
$\vec{M}_{F/A}\,\perp\,\vec{F} \qquad \mathit{\&} \qquad \vec{M}_{F/A}\,\perp\,\vec{r}_{F/A}. $
Smisao vektora $\vec{M}_{F/A}$ određen je pravilom desne ruke ili pravilom desnoga vijka.
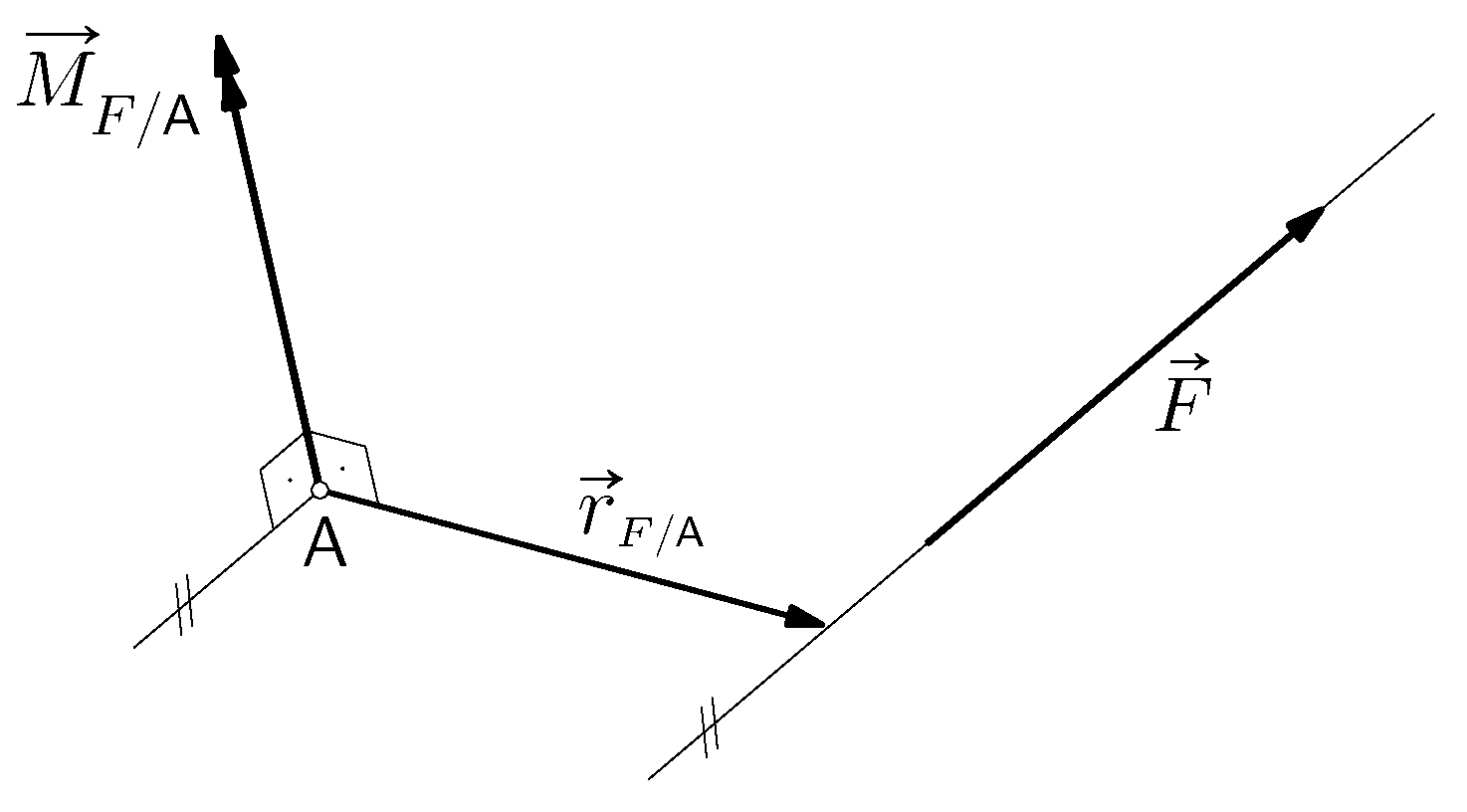
|
|
... podsjećamo: ako su vektori međusobno okomiti, njihov je skalarani umnožak jednak nuli:
$\vec{M}_{F/A}\cdot\vec{F} \,=\, 0 \qquad \mathit{\&} \qquad \vec{M}_{F/A}\cdot\vec{r}_{F/A} \,=\, 0$
0 0 |
0 0 |
(3) Intenzitet vektora $\vec{M}_{F/A}$ jednak je umnošku intenziteta vektora $\vec{F}$ i udaljenosti pravca djelovanja sile od točke $A$:
$\Big\|\vec{M}_{F/A} \Big\| \:=\: \big\|\vec{r}_{F/A}\big\|\:\big\|\vec{F}\big\|\:\sin\alpha \:=\: \big(\big\|\vec{r}_{F/A}\big\|\:\sin\alpha\big)\:\big\|\vec{F}\big\| \:=\: d\,|F|.$

Geometrijski, to je ploština paralelograma kojemu su dvije susjedne stranice $\vec{r}_{F/A}$ i $\vec{F}$.
(4) Vrh položajnoga vektora $\vec{r}_{F/A}$ može biti u bilo kojoj je točki pravca djelovanja sile $\vec{F}$:
$\vec{M}_{F/A} \:=\: \vec{r}_{F/A}\times\vec{F} \:=\: (\vec{a}_{F/A} +\vec{f})\times\vec{F} \:=\: \vec{a}_{F/A}\times\vec{F} \,+\, \underbrace{\vec{f}\times\vec{F}}_{\textstyle\vec{0}} \:=\: \vec{a}_{F/A}\times\vec{F}.$

Slijedi da je vektor sile klizni vektor, vezan za pravac — u izražavanju uvjetâ ravnoteže tijela nije bitno hvatište sile, nego samo pravac njezina djelovanja koji, naravno, prolazi hvatištem.
Primjer 3.:
Sila $\vec{F}$ intenziteta $F = 5$ djeluje na pravcu određenom točkama $A = \big(1, 0, -\!\frac{1}{2}\!\big)$ i $B = \big(\!\frac{3}{4}, -\!\frac{5}{4}, \frac{7}{8}\!\big)$, s orijentacijom od točke $A$ prema točki $B$. Izračunat ćemo moment(e) sile $\vec{F}$ u odnosu na ishodište tako da za njezine položajne vektore uzmemo vektore $\vec{r}_A$ i $\vec{r}_B$.
- položajni vektori:
(1, 0, -1/2) (3/4, -5/4, 7/8) (1, 0, -1/2) (3/4, -5/4, 7/8) |
- sila $\vec{F}$:
|
|
- moment sile $\vec{F}$ u odnosu na ishodište pomoću položajnoga vektora $\vec{r}_A = \vec{r}_{A/O}$:
|
|
- moment sile $\vec{F}$ u odnosu na ishodište pomoću položajnoga vektora $\vec{r}_B = \vec{r}_{B/O}$:
|
|
- usporedba (provjera jednakosti):
True True |
Varignonov teorem
Moment sile $\vec{F} = \displaystyle\sum_{i=0}^{n-1} \vec{F}_i$ u odnosu na točku $A$ jednak je zbroju momenata njezinih komponenata $\vec{F}_i$, $i = 0,\ldots,n\!-\!1$, u odnosu na tu točku:
$\vec{M}_{F/A} \,=\, \displaystyle\sum_{i=0}^{n-1} \vec{M}_{F_i/A}.$
Dokaz:
$\vec{M}_{F/A} \,=\, \vec{r}_{F/A} \times \vec{F} \,=\,\vec{r}_{F/A} \times \!\left\lgroup \displaystyle\sum_{i=0}^{n-1} \vec{F}_i \right\rgroup\! \,=\, \displaystyle\sum_{i=0}^{n-1} \Big(\vec{r}_{F/A} \times \vec{F}_i\Big) \,=\, \displaystyle\sum_{i=0}^{n-1} \Big(\vec{r}_{F_i/A} \times \vec{F}_i\Big) \,=\, \displaystyle\sum_{i=0}^{n-1} \vec{M}_{F_i/A}$
Primjer 4.:
Silu $\vec{F}$ prikazat ćemo kao zbroj sile $\vec{F}_0$ intenziteta $F_0 = 3$ koja djeluje na pravcu određenom točkama $A = \big(1, 0, \frac{1}{2}\!\big)$ i $B = \big(\!\frac{5}{4}, \frac{3}{4}, \frac{5}{8}\!\big)$, s orijentacijom od točke $A$ prema točki $B$, i sile $\vec{F}_1$ intenziteta $F_1 = 4$ na pravcu određenom točkama $A$ i $C = \big(\!\!-\frac{3}{4}, \frac{1}{2}, \frac{1}{2}\!\big)$, od $A$ prema $C$. Provjerit ćemo valjanost Varignonova teorema izračunavanjem momenata u odnosu na ishodište i na točku $D = (5, 5, 5)$.
Moment u odnosu na ishodište:
- položajni vektori:
(1, 0, 1/2) (5/4, 3/4, 5/8) (-3/4, 1/2, 1/2) (1, 0, 1/2) (5/4, 3/4, 5/8) (-3/4, 1/2, 1/2) |
- zadavanje sila u obliku $\vec{F}_i \,=\, F_i\,\vec{e}_i$:
|
|
- rezultanta sila $\vec{F}_0$ i $\vec{F}_1$:
|
|
- moment rezultante $\vec{F}$ u odnosu na ishodište:
|
|
- momenti sila $\vec{F}_0$ i $\vec{F}_1$ u odnosu na ishodište:
|
|
- zbroj momenata sila $\vec{F}_0$ i $\vec{F}_1$:
|
|
- usporedba momenata kao potvrda Varignonova teorema:
True True |
- grafički prikazi:
|
|
- sile $\vec{F}_0$, $\vec{F}_1$ i $\vec{F}$:
|
|
- moment rezultante $\vec{F}$:
|
|
- moment sile $\vec{F}_0$:
|
|
- moment sile $\vec{F}_1$:
|
|
- sve sile i momenti:
|
|
Momenti u odnosu na točku $D$:
(-4, -5, -9/2) (-4, -5, -9/2) |
|
|
True True |
Moment sile oko osi (ili: moment sile u odnosu na os)

Moment sile $\boldsymbol{\vec{F}}$ oko osi $\boldsymbol{o}$ jednak je momentu njezine komponente $\vec{F}{}^{\perp}$ u ravnini okomitoj na os $o$ u odnosu na probodište $P$ osi s tom ravninom:
$\vec{M}_{F/o} \,=\, \vec{M}_{F^\perp/P} \,=\, \vec{r}_{F/P} \times \vec{F}{}^{\perp}.$
Iz $\vec{F}{}^{\perp}\!\!\perp o$ i $\vec{r}_{F/P}\perp o$ slijedi $\vec{M}_{F/o} \,\|\: o$.
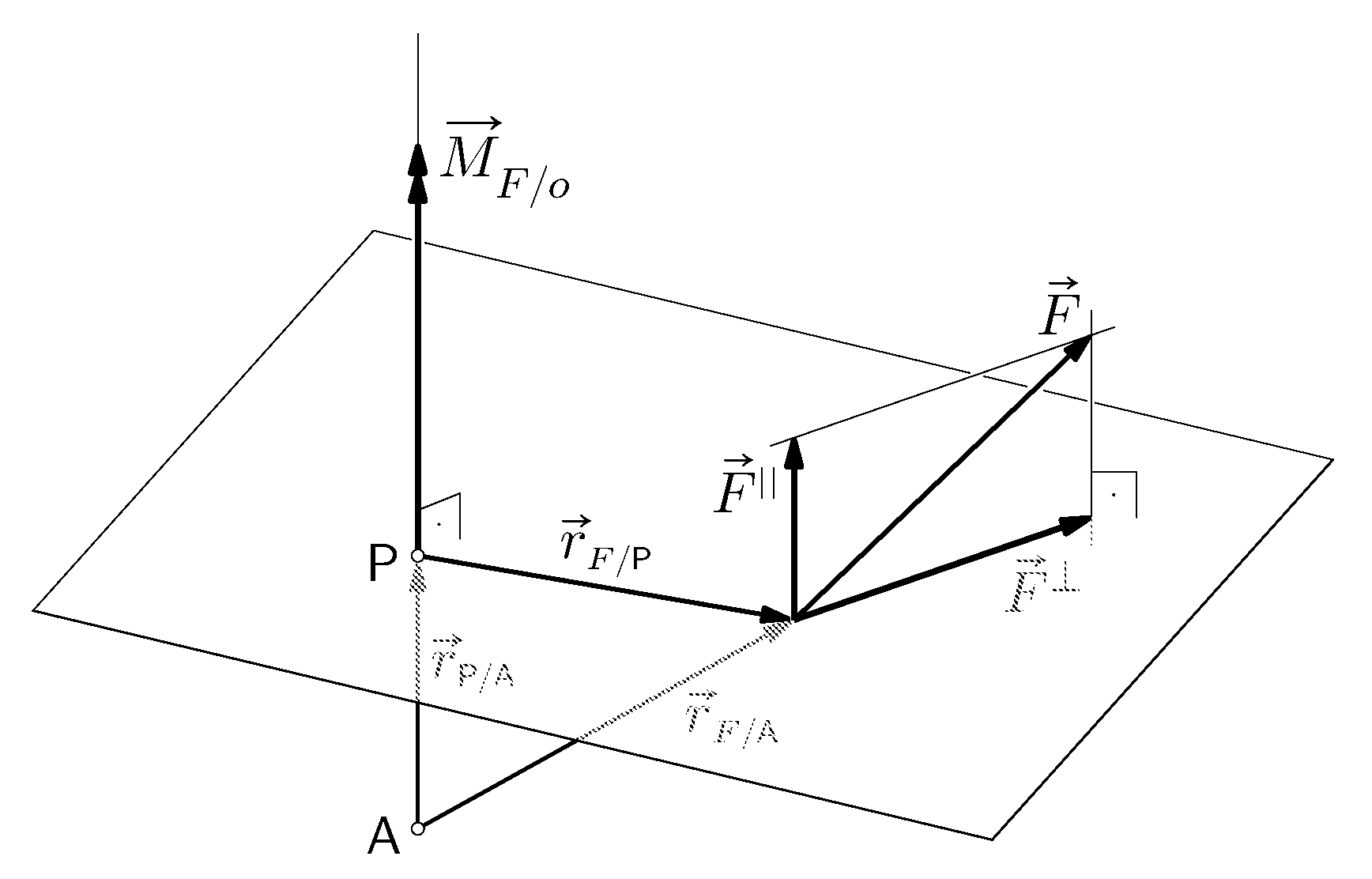
Vektor $\vec{M}_{F/o}$ može se izračunati kao (ortogonalna vektorska) projekcija na os $o$ vektora $\vec{M}_{F/A}$ momenta sile $\vec{F}$ u odnosu na bilo koju točku $A$ te osi:
$\vec{M}_{F/A} \:=\: \vec{r}_{F/A}\times\vec{F} \:=\: (\vec{r}_{P/A} + \vec{r}_{F/P}) \times \big(\vec{F}{}^{\scriptscriptstyle\|} + \vec{F}{}^{\perp} \big)$
$\phantom{\vec{M}_{F/A}} \:=\: \underbrace{\vec{r}_{P/A}\times\vec{F}{}^{\scriptscriptstyle\|}}_{\textstyle \vec{0}} \:+\: \underbrace{\vec{r}_{P/A}\times\vec{F}{}^{\perp}}_{\textstyle \perp o} \:+\: \underbrace{\vec{r}_{F/P}\times\vec{F}{}^{\scriptscriptstyle\|}}_{\textstyle \perp o} \:+\: \underbrace{\vec{r}_{F/P}\times\vec{F}{}^{\perp}}_{\textstyle \|\, o},$
$\vec{M}_{F/A}\cdot \vec{e}_o \:=\: \underbrace{\big(\vec{r}_{P/A}\times\vec{F}{}^{\perp}\big)\cdot \vec{e}_o}_{\textstyle 0} \:+\: \underbrace{\big(\vec{r}_{F/P}\times\vec{F}{}^{\scriptscriptstyle\|}\big)\cdot \vec{e}_o}_{\textstyle 0} \:+\: \big(\vec{r}_{F/P}\times\vec{F}{}^{\perp}\big)\cdot \vec{e}_o \:=\: M_{F^\perp/P} \:=\: M_{F/o},$
$\vec{M}_{F/o} \:=\: M_{F/o}\:\vec{e}_o \:=\: \big(\vec{M}_{F/A}\cdot \vec{e}_o\big)\:\vec{e}_o \:=\: \big(\vec{e}_o\cdot\vec{M}_{F/A}\big)\:\vec{e}_o \:=\: \big[\vec{e}_o \cdot \big(\vec{r}_{\!F/A} \times \vec{F}\,\big)\big]\:\vec{e}_o;$
$\vec{e}_o$ je jedinični vektor osi.
- sila $\vec{F}$:
|
|
- položajni vektor $\vec{r}_{F/A}$
|
|
- jedinični vektor osi:
|
|
- vrijednost momenta sile oko osi (skalarni moment sile oko osi):
|
|
$M_{F/o} \:=\: \vec{e}_o \cdot \big(\vec{r}_{F/A} \times \vec{F}\:\big) \:=\: \left|\begin{array}{ccc} e_{o,x} & e_{o,y} & e_{o,z} \\ x_{F/A} & y_{F/A} & z_{F/A} \\ F_x & F_y & F_z \end{array}\right| \;=\;$
|
|
- (vektorski) moment sile oko osi: $\vec{M}_{F/o} \,=\, M_{F/o}\:\vec{e}_o$:
(ispisane su njegove ortogonalne skalarne komponente)
|
|
Primjer 5.:
Izračunat ćemo moment sile $\vec{F} = \vec{\imath} - \frac{5}{2}\,\vec{\jmath} - 3\,\vec{k}$ koja prolazi točkom $A = \Big(2, \frac{1}{2}, -1\Big)$ oko osi $z$.
$\bullet$ prema definiciji:
-
- ravnina kroz hvatište sile, okomita na os $z$: $z = -1$
- probodište osi $z$ s tom ravninom: $P = (0, 0, -1)$
- $\vec{F}{}^{\perp} = \vec{\imath} - \frac{5}{2}\,\vec{\jmath}$
- $\vec{M}_{F/o} \:=\: \vec{M}_{F^\perp/P} \:=\: \vec{r}_{A/P} \times \vec{F}{}^{\perp}$
|
|
(2, 1/2, 0) (1, -5/2, 0) (2, 1/2, 0) (1, -5/2, 0) |
(0, 0, -11/2) (0, 0, -11/2) |
|
|
- moment $\vec{M}_{F/z}$ kao projekcija na os $z$ momenta $\vec{M}_{F/P}$ u odnosu na točku $P$:
(-3/2, 6, -11/2) (-3/2, 6, -11/2) |
-11/2 -11/2 |
(0, 0, -11/2) (0, 0, -11/2) |
|
|
- moment $\vec{M}_{F/z}$ kao projekcija na os $z$ momenta $\vec{M}_{F/O}$ u odnosu na točku $O$:
(-4, 5, -11/2) (-4, 5, -11/2) |
(0, 0, -11/2) (0, 0, -11/2) |
|
|
|
|
Funkcije za izračunavanje vrijednosti momenta i momenta sile $\vec{F}$ s hvatištem u točki $P$ oko osi $o$ određene točkama $A$ i $B$ s orijentacijom od $A$ prema $B$:
|
|
- sila i njezino hvatište:
|
|
- vrijednost momenta i moment oko osi $z$:
-11/2 -11/2 |
(0, 0, -11/2) (0, 0, -11/2) |
- vrijednost momenta i moment oko osi $-z$:
(predznak vrijednosti momenta se mijenja, ali njegova orijentacija ne)
11/2 11/2 |
(0, 0, -11/2) (0, 0, -11/2) |
- vrijednost momenta i moment oko osi na pravcu kroz ishodište i točku $A=(1, 2, 3)$; os je orijetirana od ishodišta prema točki $A$:
-3/4*sqrt(14) -3/4*sqrt(14) |
(-3/4, -3/2, -9/4) (-3/4, -3/2, -9/4) |
- vrijednost momenta i moment oko osi na istom pravcu, ali je os sada orijetirana od točke $A$ prema ishodištu:
3/4*sqrt(14) 3/4*sqrt(14) |
(-3/4, -3/2, -9/4) (-3/4, -3/2, -9/4) |
Moment sile oko osi iščezava ako i samo ako se os i pravac djelovanje sile sijeku (u konačnoj ili u neizmjerno dalekoj točki).
- primjerice, moment sile usporedne s osi $z$ oko osi $z$:
|
|
0 0 |
- ili, moment sile koja os $z$ siječe u točki $(0, 0, z_F)$ oko osi $z$:
|
|
0 0 |
Ortogonalne vektorske komponente momenta $\vec{M}_{F/A}$ sile $\vec{F}$ na točku $A$ su momenti $\vec{M}_{F/\bar{x}}$, $\vec{M}_{F/\bar{y}}$ i $\vec{M}_{F/\bar{z}}$ sile $\vec{F}$ u odnosu na osî $\bar{x},\,\bar{y}$ i $\bar{z}$ koje prolaze točkom $A$ usporedno s osima $x,\,y$ i $z$. Ortogonalne skalarne komponente momenta $\vec{M}_{F/A}$ su vrijednosti $M_{F/\bar{x}}$, $M_{F/\bar{y}}$ i $M_{F/\bar{z}}$ momenata $\vec{M}_{F/\bar{x}}$, $\vec{M}_{F/\bar{y}}$ i $\vec{M}_{F/\bar{z}}$, a mogu se izračunati kao skalarne projekcije momenta $\vec{M}_{F/A}$ na osî $\bar{x},\,\bar{y}$ i $\bar{z}$ ili na osî $x,\,y$ i $z$. Isto se tako ortogonalne vektorske komponente momenta $\vec{M}_{F/A}$ mogu izračunati kao njegove vektorske projekcije na osî $\bar{x},\,\bar{y}$ i $\bar{z}$ ili na osî $x,\,y$ i $z$.
|
|
|
|
|
|
|
|
Primjer 6.:
Sila $\vec{F} = 5\,\vec{\imath} - \vec{\jmath} + 2\, \vec{k}$ djeluje u ishodištu. Izračunat ćemo moment te sile u odnosu na točku $A = \big(3, \frac{11}{3}, -\frac{1}{3}\big)$ i rastaviti ga u ortogonalne komponente.
|
|
- $\vec{M}_{F/A}$ :
|
|
- ortogonalne komponente:
|
|
|
|
Moment sprega
Spregom sila ili samo spregom nazivaju se dvije sile, $\vec{F}$ i $-\vec{F}$, na usporednim pravcima, jednakih intenziteta, ali suprotnih orijentacija.
Moment sprega je vektor dobiven zbrajanjem vektorâ momenata sila sprega u odnosu na istu točku:
$\vec{M}_{\pm F} \:=\: \vec{r}_{F/A}\times\vec{F} \,+\, \vec{r}_{(-F)/A}\times (-\vec{F}) \:=\: [\vec{r}_{(-F)/A} + \vec{s}]\times\vec{F} \,-\, \vec{r}_{(-F)/A}\times\vec{F} \:=\: \vec{r}_{(-F)/A}\times\vec{F} \,+\, \vec{s}\times\vec{F} \,-\, \vec{r}_{(-F)/A}\times\vec{F} \:=\: \vec{s}\times\vec{F}$
ili
$\vec{M}_{\pm F} \:=\: \vec{r}_{F/A}\times\vec{F} \,+\, \vec{r}_{(-F)/A}\times (-\vec{F}) \:=\: \vec{r}_{F/A}\times\vec{F} \,+\, [\vec{r}_{F/A} + (-\vec{s})]\times(-\vec{F}) \:=\: \vec{r}_{F/A}\times\vec{F} \,-\, \vec{r}_{F/A}\times\vec{F} \,+\, (-\vec{s})\times(-\vec{F}) \:=\: \vec{s}\times\vec{F}.$

Slijedi da je vektor $\vec{M}_{\pm F}$ jednak vektorskom umnošku položajnoga vektora jedne sile sprega u odnosu na drugu i vektora prve sile; položajni vektor jedne sile u odnosu na drugu vektor je s početkom u bilo kojoj točki pravca druge sile i s vrhom u bilo kojoj točki pravca prve sile. Također slijedi da je vektor $\vec{M}_{\pm F}$ okomit na ravninu koji određuju pravci djelovanja sila $\vec{F}$ i $-\vec{F}$.
Budući da položajni vektor $\vec{s}$ ne ovisi o izboru točke $A$, o njoj ne ovisi ni moment sprega. Moment sprega možemo stoga smjestiti u bilo koju točku — vektor momenta sprega je slobodni vektor.
Primjer 7.:
Izračunat ćemo moment sprega sila $\vec{F} = 3\,\vec{\imath} - \vec{\jmath} + \vec{k}$ i $-\vec{F}$ s hvatištima u točkama $A = (-1, 1, 0)$ i $B = (0, 3, 1)$.
|
|
- $\vec{M}_{\pm F} \,=\, \vec{M}_{F/O} + \vec{M}_{(-F)/O}$
(-1, 1, 4) (-3, -3, 6) (-4, -2, 10) (-1, 1, 4) (-3, -3, 6) (-4, -2, 10) |
|
|
- $\vec{M}_{\pm F} \,=\, \vec{M}_{F/B} \,=\, \vec{r}_{F/B}\times\vec{F} \,=\, \vec{r}_{A/B}\times\vec{F}$
(-4, -2, 10) (-4, -2, 10) |
|
|
- $\vec{M}_{\pm F} \,=\, \vec{M}_{(-F)/A} \,=\, \vec{r}_{(-F)/A}\times(-\vec{F}) \,=\, \vec{r}_{B/A}\times(-\vec{F})$
(-4, -2, 10) (-4, -2, 10) |
|
|
|
|
Funkcija za izračunavanje momenta sprega sila $\vec{F}$ i $-\vec{F}$ s hvatištima u točkama $A$ i $B$:
|
|
(-4, -2, 10) (-4, -2, 10) |
Zamislit ćemo da se intenziteti sila sprega povećavaju i da se pravci njihova djelovanja približavaju, ali tako da se moment sprega ne mijenja. U „graničnom” trenutnu, kada intenziteti sila postanu neizmjerno veliki, a udaljenost pravaca neizmjerno malena, moment tih sila nazivamo koncentriranim momentom.
Uvjeti ravnoteže tijela na koje djeluju koncentrirane sile $\big\{\vec{F}_i\big\}_{i = 0}^{n-1}$ i koncentrirani momenti $\big\{\vec{M}_i\big\}_{j = 0}^{m-1}$
Sada, kad smo upoznali pojam momenta sile, možemo izreći uvjete ravnoteže tijela:
Tijelo na koje djeluju sile $\vec{F}_0,\,\vec{F}_1,\,\ldots\,,\,\vec{F}_{n-1}$ i momenti $\vec{M}_0,\,\vec{M}_1,\,\ldots\,,\,\vec{M}_{m-1}$ je u ravnoteži ako iščezavaju zbroj svih sila i zbroj svih momenata, pri čemu zbroj momenata obuhvaća momente svih sila u odnosu na neku, bilo koju točku i sve koncentrirane momente.
Uvjete ravnoteže možemo izraziti u vektorskom i u skalarnom obliku.
U vektorskom su obliku uvjeti izraženi dvjema jednadžbama:
1. uvjet: iščezavanje zbroja svih sila
$\displaystyle\sum_{i = 0}^{n-1} \vec{F}_i \:=\: \vec{0}$,
2. uvjet: iščezavanje zbroja svih momenata — momenata sila u odnosu na bilo koju točku (ishodište, primjerice) i koncentriranih momenata
$\displaystyle\sum_{i = 0}^{n-1} \vec{r}_{F_i/O}\times\vec{F}_i \,+\, \displaystyle\sum_{j = 0}^{m-1} \vec{M}_j \:=\: \vec{0}$.
Budući da su ortogonalne komponente vektora međusobno linearno nezavisne, svaku vektorsku jednadžbu možemo zamijeniti trima skalarnim jednadžbama (po skalaranim komponentama), pa skalarni iskaz uvjeta ravnoteže sadrži šest jednadžbi (dvije skupine po tri jednadžbe):
1. uvjet: iščezavanje zbroja svih sila
$\displaystyle\sum_{i = 0}^{n-1} F_{i,x} \:=\: 0$,
$\displaystyle\sum_{i = 0}^{n-1} F_{i,y} \:=\: 0$,
$\displaystyle\sum_{i = 0}^{n-1} F_{i,z} \:=\: 0$;
2. uvjet: iščezavanje zbroja svih momenata — momenata sila u odnosu na bilo koju točku (ishodište, primjerice) i koncentriranih momenata
$\displaystyle\sum_{i = 0}^{n-1} (y_i\,F_{i,z} - z_i\,F_{i,y}) \,+\, \displaystyle\sum_{j = 0}^{m-1} M_{j,x} \:=\: 0$,
$\displaystyle\sum_{i = 0}^{n-1} (-x_i\,F_{i,z} + z_i\,F_{i,x}) \,+\, \displaystyle\sum_{j = 0}^{m-1} M_{j,y} \:=\: 0$,
$\displaystyle\sum_{i = 0}^{n-1} (x_i\,F_{i,y} - y_i\,F_{i,x}) \,+\, \displaystyle\sum_{j = 0}^{m-1} M_{j,z} \:=\: 0$.
|
|