Mehanika 1.
Stranica predmeta na Merlinu (obavijesti, primjeri kolokvija i ispita)
Udžbenik:
Heinrich Werner: Mehanika I – Statika, Hrvatski savez građevinskih inženjera, Zagreb, 2007. (prikaz knjige)
[Napomene o programskom kôdu u SageMath-u:
Tekst poput ovoga, pisan slovima sans serif (bez vitica), odnosi se ponajprije na programski kôd.
Ćelije u kojima je prvi redak %auto ne trebate izvoditi ( evaluate ); one se izvode „same” pri otvaranju radnoga lista.
Funkcije, programska realizacija kojih nije bitna za razumijevanje gradiva Mehanike 1., „skrivene” su, a opisan je samo način njihova pozivanja.]
|
|
Mehanika
Mehanika je znanost o općim zakonima ravnoteže i gibanjâ tijelâ izloženih djelovanju sila.
Klasična mehanika može se podijeliti
- prema obilježjima zadaća koje se proučavaju i rješavaju na
- kinematiku ili geometriju gibanjâ (neovisno o njihovim uzrocima) i na
- dinamiku, koja se bavi utjecajem djelovanja sila, a dalje se dijeli na
- statiku, središnji pojam koje je ravnoteža, odnosno „mirovanje” uz djelovanje sila, te na
- kinetiku, počela koje su sile kao uzroci promjena gibanjâ i tromosti masa koje teže održanju nepromijenjenog i nepromjenjivog stanja;
- prema geometrijskim i materijalnim svojstvima predmeta proučavanja na
- mehaniku materijalne točke i sistema materijalnih točaka,
- mehaniku krutih tijela i njihovih sistema,
- mehaniku deformabilnih tijela i njihovih sistema te
- mehaniku fluida (tekućina i plinova).
(Iako je navedena podjela prema obilježjima proučavanih zadaća prirodna (jer značenje je grčke riječi dýnamis [$\delta\acute{\upsilon}\nu\alpha\mu\iota\varsigma$] sila), danas je uvriježenija podjela mehanike na statiku, u koju vas uvodi Mehanika 1., te kinematiku i dinamiku (a sadržajno tek kinetiku; kao da u statici nema sila), s kojima ćete se upoznati u Mehanici 2.)
Realno čvrsto tijelo (tijelo u čvrstom agregatnom stanju) skup je čestica međusobne udaljenosti kojih se bitno ne mijenjaju pri djelovanju sila i drugih utjecaja (poput topline). Čvrsta se tijela modeliraju kao
- (materijalne) točke,
- (apsolutno) kruta tijela udaljenosti točaka kojih se zaista ne mijenjaju te
- defomarbilna tijela koja mijenjaju oblik (ipak, u granicama prepoznatljivosti).
(Model je umjetna—fizička ili matematička—tvorevina izrađena kao zamjena za izdvojeni složeni isječak stvarnosti. Modeli se oblikuju nizovima apstrakcija i idealizacija. Model nema sva svojstva onoga što predočava, nego je tek aproksimacija stanja, građe ili ponašanja predočenoga.)
Statika je grana mehanike u kojoj se proučava ravnoteža tijelâ, što znači da se istražuju djelovanja sila na tijela koja miruju (u odnosu na referentni inercijalni koordinatni sustav) i koja pod djelovanjem sila ostaju u stanju mirovanja. (U Mehanici 1. ograničit ćemo se na materijalne točke i na kruta tijela te na sisteme točaka i krutih tijela; deformabilnim tijelima bavit ćete se sljedećih godina u Otpornostima materijala i Građevnim statikama, a tekućinama u Mehanici tekućina.)
Pojam sile
[Natuknice možete naći i u datoteci Pojam sile u Bilješkama i skicama s predavanja]
Sila je fizikalna veličina kojom se opisuje uzajamno djelovanje tijelâ. Pod silom se, prema Lagrangeu [Analitička mehanika, 1788.] „razumije općenito uzrok, bez obzira na njegovu vrstu, koji priopćava ili teži priopćiti gibanje tijelima na koja djeluje; štoviše, priopćena količina gibanja, ili količina gibanja koja se može priopćiti, ono je čime silu treba prikazati. U stanju ravnoteže sila nema stvaran učinak; ona samo namiče težnju gibanju; ipak, uvijek se može mjeriti učinkom koji bi stvorila kad ne bi bila zapriječena.”
Sile se dijele
- prema dosegu na
- sile kratkoga dosega, koje djeluju na „dodirnoj” površini, stvarnoj ili zamišljenoj, poput kontaktnih sila između dvaju tijela ili unutarnjih sila (u čvrstom tijelu),
- sile dalekoga dosega, koje djeluju na cijelo tijelo, poput gravitacijskih, električnih ili magnetskih;
- prema području djelovanja na
- distribuirane ili raspodijeljene (linijske, plošne, zapreminske) te
- koncentrirane;
- prema smislu djelovanja na
- privlačne ili vlačne ili sile zatezanja,
- odbojne ili tlačne ili sile pritiska.
Sile kratkoga dosega su plošne, a sile dalekog dosega zapreminske; koncentrirane i raspodijeljene linijske sile korisna su idealizacija.
Koncentrirana sila je sila koja djeluje u točki, a ima pravac i smisao djelovanja (ili orijentaciju) te intenzitet. Intenzitet sile je, po definiciji, kao i duljina dužine, pozitivna veličina. Ako je na pravcu njezina djelovanja dogovorno utvrđena pozitivna orijentacija, smisao djelovanja sile možemo s pomoću predznaka priključiti intenzitetu pa ćemo govoriti o vrijednosti sile: sila, kojoj je smisao djelovanja suprotan od pozitivnoga, imat će negativnu vrijednost. Točka, u kojoj sila djeluje, naziva se njezinim hvatištem.
Prema drugom Newtonovu zakonu, djeluje li na nepomično tijelo jedna sila, ono će se početi gibati po pravcu i u smislu djelovanja te sile. Djeluje li na tijelo više sila, ta se djelovanja mogu međusobno poništiti, pa će tijelo ostati nepomičnim — za statiku, prema tome, jedna sila nije dovoljna. Za sistem sila, koje djeluju na tijelo tako da ono ostaje u stanju mirovanja (u odnosu na neki inercijalni sustav), kažemo da je uravnotežen.
Za iskaz uvjetâ ravnoteže treba objasniti što znači izraz „poništavanje djelovanja sila”, a za to pak treba uvesti postupak sastavljanja sila (na ovom predavanju) i pojam momenta sile (na sljedećem predavanju).
Zbrajanje sila
Godine 1608. Simon Stevin je u dodatku knjige Počela umijeća vaganja, naslovljenom O užadi koja nosi terete, uveo pravilo paralelograma sila i, potom, pravilo trokuta sila, kao osnove postupka rastavljanja sile u dvije komponente na zadanim pravcima koji prolaze njezinim hvatištem, pri čemu ta dva pravca i pravac djelovanja sile leže u jednoj ravnini.

Sila u užetu GF, intenzitet koje je jednak težini obješenoga tereta i proporcionalan duljini dužine CI, može se zamijeniti silama u užadi CD i CE; intezitet sile u užetu CD proporcionalan je duljini dužine CH, dobivene povlačenjem pravca paralelnog užetu CE kroz točku I.
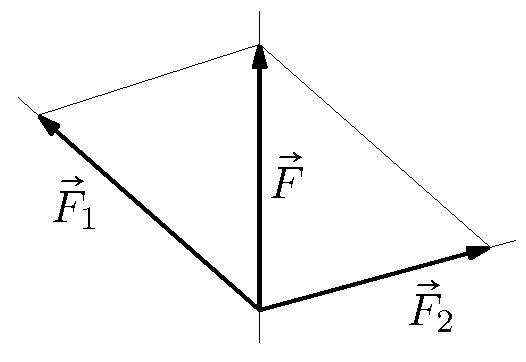
Dakle, silu $\vec{F}$ grafički rastavljamo u komponente $\vec{F}_1$ i $\vec{F}_2$ na dvama različitim pravcima kroz njezino hvatište (rep strelice kojom smo prikazali silu $\vec{F}$) tako da njezinim šiljkom povučemo pravce usporedne zadanim pravcima, pa su sile $\vec{F}_1$ i $\vec{F}_2$ dvije susjedne stranice paralelograma čija je dijagonala $\vec{F}$. Zadaća je rješiva samo ako sila koju rastavljamo i pravci njezinih komponenata leže u istoj ravnini; postoji li rješenje, ono je samo jedno.
Može se reći i da je, obratno, sila $\vec{F}$ nastala sastavljanjem ili zbrajanjem sila $\vec{F}_1$ i $\vec{F}_2$ koje djeluju u istoj točki,
$$\vec{F} \,=\, \vec{F}_1 + \vec{F}_2;$$
rezultanta $\vec{F}$ silâ $\vec{F}_1$ i $\vec{F}_2$ dijagonala je paralelograma razapetoga silama $\vec{F}_1$ i $\vec{F}_2$. Zadaća zbrajanja dviju sila koje imaju isto hvatište uvijek je rješiva, a dobivena rezultanta leži, jasno je, u ravnini koju razapinju pravci djelovanja tih sila.
Pravilo paralelograma vrijedi i za sastavljanje ili za rastavljanje drugih fizikalnih veličina odredenih intenzitetom, pravcem i smislom, poput pomaka, brzine i ubrzanja. Zajednička svojstva tih veličina obuhvaćena su u apstraktnom matematičkom pojmu vektora (MPZI_predavanje_05).
Budući da su duljine usporednih stranica paralelograma jednake, umjesto paralelograma može se konstruirati trokut. Pritom se, međutim, jedna sila „pomiče” s pravca svoga djelovanja na paralelni pravac, pa se položajni odnosi sila više ne mogu očitati iz crteža.

Usporedba lijeve i desne polovine paralelograma sila s trokutima sila pokazuje da je zbrajanje sila komutativno:
$$\vec{F}_1 + \vec{F}_2 \,=\, \vec{F}_2 + \vec{F}_1.$$
Djeluju li u istom hvatištu tri sile $\vec{F}_1,\:\vec{F}_2$ i $\vec{F}_3$, njihovu rezultantu možemo naći tako da opisanim postupkom zbrojimo sile $\vec{F}_1$ i $\vec{F}_2$, $\vec{F}_{1,2} = \vec{F}_1 + \vec{F}_2$, te da potom zbrojimo dobivenu silu $\vec{F}_{1,2}$ i silu $\vec{F}_3$:
$$\vec{F} \,=\, (\vec{F}_{1} + \vec{F}_2) + \vec{F}_3 \,=\, \vec{F}_{1,2} + \vec{F}_3.$$
Pokazat ćemo kasnije da ćemo istu rezultantu $\vec{F}$ dobiti ako prvo zbrojimo sile $\vec{F}_2$ i $\vec{F}_3$, a potom njihov zbroj $\vec{F}_{2,3}$ pribrojimo sili $\vec{F}_1$:
$$\vec{F} \,=\, \vec{F}_{1} + (\vec{F}_2 + \vec{F}_3) \,=\, \vec{F}_1 + \vec{F}_{2,3}.$$
Drugim riječima, zbrajanje sila je asocijativno, pa u izrazu za zbroj triju sila zagrade ne moramo pisati:
$$\vec{F} \,=\, \vec{F}_{1} + \vec{F}_2 + \vec{F}_3.$$
Sile $\vec{F}_1,\:\vec{F}_2$ i $\vec{F}_3$ mogu, ali i ne moraju ležati u jednoj ravnini. Ako su u jednoj ravnini, tada je, naravno, i njihova rezultanta u toj ravnini. Ako pak tri sile nisu u jednoj ravnini, njihova je rezultanta prostorna dijagonala paralelepipeda koji razapinju.
Obratno (ali tek djelomice), prolaze li kroz hvatište sile tri pravca koji nisu u istoj ravnini, sila se može rastaviti u komponente na tim pravcima; rastav je samo jedan. Ako su pravci u jednoj ravnini i ako je i sila u toj ravnini, zadaća rastavljanja je rješiva, ali rješenje ima bezbroj; ako pak sila nije u ravnini pravaca, zadaća nije rješiva.
Grafički prikaz zbroja niza sila, koji je poopćenje trokuta sila, naziva se poligonom sila.
Za algebarsko baratanje silama pogodno je rastaviti ih u tri međusobno okomite komponente, usporedne s osima desnoga Kartezijeva ortogonalnog koordinatnog sustava. I obratno, opću je silu pogodno zadati trima komponentama, usporednima s osima koordinatnoga sustava:
$$\vec{F} \,=\, \vec{F}_x + \vec{F}_y + \vec{F}_z.$$
Komponente usporedne s osima zadajemo kao umnoške njihovih vrijednosti i jediničnih vektora $\vec{\imath},\:\vec{\jmath}$ i $\vec{k}$ na osima $x,\,y$ i $z$,
$$\vec{F}_x \,=\, F_x\,\vec{\imath}, \quad \vec{F}_y \,=\, F_y\,\vec{\jmath} \quad\text{i}\quad \vec{F}_z \,=\, F_z\,\vec{k},$$
pa je
$$\vec{F} \:=\: F_x\,\vec{\imath} \,+\, F_y\,\vec{\jmath} \,+\, F_z\,\vec{k}\,;$$
primjerice, $\vec{F} \:=\: 2\,\vec{\imath} \,+\,3\,\vec{\jmath} \,+\,\vec{k}$:
(2, 3, 1) (2, 3, 1) |
(U programskom ćemo kôdu vektore ponajčešće označavati dvostrukim slovom: varijabla FF programska je realizacija sile $\vec{F}$.)
Grafički prikaz:
- silu crtamo pozivom funkcije
f_arrow (ff, tail = (0, 0, 0), scale = 1, color = 'blue', thickness = 1)
- ff — vektor sile
- tail — hvatište sile
- [množenjem vrijednošću scale može se promijeniti duljina prikaza vektora sile (trebat će nam na sljedećim predavanjima)]
|
|
- os $z$ može biti orijentirana prema gore ili prema dolje:
show_zup (plt, axes = False, axis_length = 1, frame = False, rho = 0)
show_zdown (plt, axes = False, axis_length = 1, frame = False, rho = 0)
- plt — slika
- axes — ako je True, prikazuju se osi koordinatnoga sustava: $x$ – crveno, $y$ – narančasto, $z$ – žuto
- axis_length — duljina osî, ako se prikazuju
- frame — ako je True, prikazuje se „okvir”
- rho — kut rotacije prikaza oko osi $z$
|
|
|
|
Vrijednosti $F_x,\: F_y$ i $F_z$ u $\vec{F} = F_x\,\vec{\imath} + F_y\,\vec{\jmath} + F_z\,\vec{k}$ nazivamo ortogonalnim skalarnim komponentama sile $\vec{F}$ ili, ako je iz konteksta jasno, sažetije, skalarnim komponentama.
Skalarne su komponente sile, uz indeksiranje u SageMath-u:
$F_x = F_{\,0}$, $F_y = F_{\,1}$, $F_z = F_{\,2}$
2 3 1 2 3 1 |
|
|
3 3 |
Kako bismo istaknuli njihov vektorski karakter, komponente
$\vec{F}_x \,=\, F_x\cdot \vec{\imath} \,=\, F_{\,0}\cdot \vec{\imath}$,
$\vec{F}_y \,=\, F_y\cdot \vec{\jmath} \,=\, F_{\,1}\cdot\vec{\jmath}$ i
$\vec{F}_z \,=\, F_z\cdot \vec{k} \,=\, F_{\,2}\cdot \vec{k}$
sile $\vec{F} = \vec{F}_x + \vec{F}_y + \vec{F}_z$ nazivamo i njezinim (ortogonalnim) vektorskim komponentama.
Vektorske su komponente sile:
|
|
(2, 0, 0) (0, 3, 0) (0, 0, 1) (2, 0, 0) (0, 3, 0) (0, 0, 1) |
|
|
|
|
Još jedan primjer:
(4, 2, -3) (4, 2, -3) |
4 2 -3 4 2 -3 |
(4, 0, 0) (0, 2, 0) (0, 0, -3) (4, 0, 0) (0, 2, 0) (0, 0, -3) |
|
|
|
|
„Simboličke” sile upotrebljavat ćemo za prikaze i izvode „općih” izraza:
force (ff = 'F')
- ff — oznaka sile (znak ili niz znakova)
(F0, F1, F2) (F0, F1, F2) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Svojstva zbrajanja sila pojasnit ćemo, ilustrirati, „dokazati” i dopuniti s pomoću nekoliko primjera.
(Iako su sile koje zbrajamo zadane komponentama (i SageMath, u pozadini, računa s njima), za sada treba zamišljati da se zbrajanje provodi „grafički”, s pomoću paralelograma ili trokuta sila. O komponentama rezultante još ne znamo ništa.)
Primjer 1.:
Komutativnost zbroja sila
|
|
- paralelogram sila:
|
|
- trokut sila:
- $\vec{F}_{0,1} \,=\, \vec{F}_0 + \vec{F}_1$
|
|
- hvatište sile $F_1$ pomiče se u vrh sile $F_0$
- točka u kojoj je vrh vektora sile:
head (ff, tail = (0, 0, 0))
$\diamond$ tail — hvatište sile ff
|
|
- promjena redoslijeda sila: $\vec{F}_{1,0} \,=\, \vec{F}_1 + \vec{F}_0$
|
|
- hvatište sile $F_0$ pomiče se u vrh sile $F_1$
|
|
- zbrajanje sila je komutativno: $\vec{F}_0 + \vec{F}_1 \,=\, \vec{F}_1 + \vec{F}_0 \,=\, \vec{F}$
True True |
- usporedite sljedeću sliku s ranijim (i ispod nje ponovljenim) prikazom paralelograma sila...
|
|
|
|
Primjer 2.:
Paralelepiped sila
|
|
- ako tri sile (s istim hvatištem) nisu u jednoj ravnini, njihova je rezultanta prostorna dijagonala paralelepipeda koji te sile razapinju:
|
|
Primjer 3.:
Asocijativnost zbroja sila
(2, 0, 0) (0, 4, 0) (0, 0, 3) (2, 0, 0) (0, 4, 0) (0, 0, 3) |
- zbrojit ćemo sile $\vec{F}_0$ i $\vec{F}_1$, pa potom njihovu zbroju $\vec{F}_{0,1}$ pribrojiti silu $\vec{F}_2$:
$\vec{F} \:=\: (\vec{F}_0 + \vec{F}_1) \,+\, \vec{F}_2 \:=\: \vec{F}_{0,1} \,+\, \vec{F}_2$
|
|
- prikaz pomoću paralelogramâ sila:
|
|
- prikaz pomoću poligona sila:
|
|
- sili $F_0$ pribrojit ćemo zbroj $F_{1,2}$ sila $F_1$ i $F_2$:
$\vec{F} \:=\: \vec{F}_0 \,+\, (\vec{F}_1 + \vec{F}_2) \:=\: \vec{F}_0 \,+\, \vec{F}_{1,2}$
|
|
- prikaz pomoću paralelogramâ sila:
|
|
- prikaz pomoću poligona sila:
|
|
- zaključak: $(\vec{F}_0 + \vec{F}_1) \,+\, \vec{F}_2 \:=\: \vec{F}_0 \,+\, (\vec{F}_1 + \vec{F}_2)$
True True |
- budući da vrijedi i zakon komutativnosti, možemo zbrojiti sile $\vec{F}_0$ i $\vec{F}_2$, pa dobivenoj sili $\vec{F}_{0,2}$ pribrojiti silu $\vec{F}_1$ (ili sili $\vec{F}_1$ pribrojiti silu $\vec{F}_{0,2}$):
$\vec{F} \:=\: (\vec{F}_0 + \vec{F}_2) \,+\, \vec{F}_1 \:=\: \vec{F}_{0,2} \,+\, \vec{F}_1 \:=\: \vec{F}_1 \,+\, \vec{F}_{0,2}$
True True |
|
|
- prikaz pomoću paralelogramâ sila:
|
|
- prikaz pomoću poligona sila:
|
|
- zaključak: $(\vec{F}_0 + \vec{F}_2) \,+\, \vec{F}_1 \:=\: \vec{F}_0 \,+\, \vec{F}_1 + \vec{F}_2$
True True |
Primjenom svojstava komutativnosti i asocijativnosti zbrajanja može se pokazati da je rezultanta niza sila sila kojoj su komponente rezultante odgovarajućih komponenata sila niza:
$\vec{R} \;=\: \displaystyle\sum_{i = 0}^{n-1} \:\vec{F}_i \:=\: \displaystyle\sum_{i = 0}^{n-1} \:F_{i,x}\,\vec{\imath} \,+\, \displaystyle\sum_{i = 0}^{n-1} \:F_{i,y}\,\vec{\jmath} \,+\, \displaystyle\sum_{i = 0}^{n-1} \:F_{i,z}\,\vec{k} \:=\: \vec{\imath}\:\displaystyle\sum_{i = 0}^{n-1} \:F_{i,x} \,+\, \vec{\jmath}\:\displaystyle\sum_{i = 0}^{n-1} \:F_{i,y} \,+\,\vec{k}\:\displaystyle\sum_{i = 0}^{n-1} \:F_{i,z}$
(2, 0, 0) (0, 4, 0) (0, 0, 3) (2, 4, 3) (2, 0, 0) (0, 4, 0) (0, 0, 3) (2, 4, 3) |
Primjer 4.:
Poligon sila
(3, 3/2, 0) (0, 0, 2) (0, -2, 0) (-7/2, 4, -5/2) (0, -1, -2) (3, 3/2, 0) (0, 0, 2) (0, -2, 0) (-7/2, 4, -5/2) (0, -1, -2) |
(-1/2, 5/2, -5/2) (-1/2, 5/2, -5/2) |
|
|
- redoslijed sila u poligonu sila nije važan (posljedica zakonâ komutativnosti i asocijativnosti):
|
|
- polygon_of_forces_plot3d (forces, tail = (0, 0, 0), color = 'blue')
- forces — lista sila
- tail — hvatište prve sile
Poligon sila je zatvoren ako i samo ako zbroj sila iščezava $\displaystyle\left(\sum_{i=0}^{n-1} \vec{F}_i \,=\, \vec{0} \right)$.
Primjer 4.:
Poligon sila (nastavak)
- zbroj sila ne iščezava:
(-1/2, 5/2, -5/2) (-1/2, 5/2, -5/2) |
$\Rightarrow$ poligon sila nije zatvoren:
|
|
- dodat ćemo silu $F_5$:
|
|
- sada zbroj sila iščezava:
(0, 0, 0) (0, 0, 0) |
$\Rightarrow$ poligon sila je zatvoren:
|
|
Budući da su vektorske komponente sile međusobno linearno nezavisne,
$\displaystyle\sum_{i = 0}^{n-1} \:\vec{F}_i \:=\: \vec{0}$ $\Longleftrightarrow$ $\displaystyle\sum_{i = 0}^{n-1} \:F_{i,x} \,=\, 0 \quad \mathit{\&} \quad \displaystyle\sum_{i = 0}^{n-1} \:F_{i,y} \,=\, 0 \quad \mathit{\&} \quad \displaystyle\sum_{i = 0}^{n-1} \:F_{i,z} = 0$.
Dakle, zbroj sila iščezava ako i samo ako su sve njegove komponente (skalarne, a time i vektorske) jednake nuli.
0 0 0 0 0 0 |
0 0 0 0 0 0 |
Ako zbroj sila koje djeluju na materijalnu točku iščezava, kažemo da je točka u ravnoteži ili da je uravnotežena.
Množenje sile brojem
Pri množenju sile brojem $c$ sve se njezine komponente množe tim brojem:
$c\,\vec{F} \,=\, c\, (F_x\,\vec{\imath} + F_y\,\vec{\jmath} + F_z\,\vec{k}) \,=\, c\,F_x\,\vec{\imath} + c\,F_y\,\vec{\jmath} + c\,F_z\,\vec{k}$.
Ako je $c > 0$, smisao se djelovanja sile ne mijenja:
(1, 3, 2) (2, 6, 4) (1, 3, 2) (2, 6, 4) |
(1, 0, 0) (0, 3, 0) (0, 0, 2) (1, 0, 0) (0, 3, 0) (0, 0, 2) |
(2, 0, 0) (0, 6, 0) (0, 0, 4) (2, 0, 0) (0, 6, 0) (0, 0, 4) |
|
|
Ako je $c < 0$, smisao se djelovanja sile mijenja. Posebno, $-\vec{F} \,=\, -1\cdot\vec{F} \,=\, -F_x\,\vec{\imath} - F_y\,\vec{\jmath} - F_z\,\vec{k}$:
(1, 3, 2) (-1, -3, -2) (1, 3, 2) (-1, -3, -2) |
|
|
Oduzimanje sila
Oduzimanje sile $\vec{F}_1$ od sile $\vec{F}_0$ definira se kao zbrajanje sila $\vec{F}_0$ i $-\vec{F}_1$:
$\vec{F}_0 - \vec{F}_1 \,=\, \vec{F}_0 + (-\vec{F}_1)$
|
|
|
|
|
|
True True |
Još neka svojstva sila
Intenzitet sile je „duljina” (euklidska norma) vektora sile:
$\|\vec{F}\,\| \,=\, |F| \,=\, \sqrt{F_x^2 + F_y^2 + F_z^2} \,=\, \displaystyle\sqrt{\sum_{i=0}^2 F_i^2} \,=\, \displaystyle\sqrt{\sum_{i=0}^2 F_i\cdot F_i} \,=\, \sqrt{\vec{F}\cdot\vec{F}}$
|
|
|
|
|
|
(2.00000000000000, 3.00000000000000, 1.00000000000000) 3.74165738677394 (2.00000000000000, 3.00000000000000, 1.00000000000000) 3.74165738677394 |
Intenzitet sile pomnožene brojem dan je izrazom $\|c\, \vec{F}\| \,=\, |c|\, \|\vec{F}\|$:
(4, 6, 2) (4, 6, 2) |
|
|
True True |
(-4, -6, -2) (-4, -6, -2) |
|
|
True True |
Jedinična sila na pravcu i u smislu djelovanja sile $\vec{F}$ dobiva se množenjem sile recipročnom vrijednošću njezina intenziteta:
$\vec{f}_{\!0} \,=\, \dfrac{1}{\|\vec{F}\,\|}\,\vec{F} \,=\, \dfrac{\vec{F}}{\|\vec{F}\,\|} \,=\, \dfrac{F_x\,\vec{\imath} + F_y\,\vec{\jmath} + F_z\,\vec{k}}{\|\vec{F}\,\|} \,=\, \dfrac{F_x}{\|\vec{F}\,\|} \vec{\imath} + \dfrac{F_y}{\|\vec{F}\,\|} \vec{\jmath} + \dfrac{F_z}{\|\vec{F}\,\|} \vec{k} \,=\, f_{0,x}\,\vec{\imath} + f_{0,y}\,\vec{\jmath} + f_{0,z}\,\vec{k}$
|
|
|
|
|
|
1 1 |
|
|
1 1 |
(0.534522483824849, 0.801783725737273, 0.267261241912424) 1.00000000000000 (0.534522483824849, 0.801783725737273, 0.267261241912424) 1.00000000000000 |
|
|
Zadavanje sile pomoću vrijednosti i jediničnoga vektora na pravcu njezina djelovanja:
$\vec{F} \,=\, F\:\vec{e}_0 \,=\, F\:(e_{0,x}\,\vec{\imath} + e_{0,y}\,\vec{\jmath} + e_{0,z}\,\vec{k}) \,=\, F\,e_{0,x}\,\vec{\imath} + F\,e_{0,y}\,\vec{\jmath} + F\,e_{0,z}\,\vec{k}$
|
|
- ako je vrijednost sile pozitivna, smisao je njezina djelovanja jednak smislu jediničnoga vektora:
|
|
|
|
7/3 7/3 |
|
|
- ako je vrijednost sile negativna, smisao je njezina djelovanja suprotan smislu jediničnoga vektora:
|
|
|
|
- ali, kako je intenzitet sile pozitivan broj, ako je $F < 0$, intenzitet je $|F|$:
7/3 7/3 |
- budući da se jednična sila izračuvana množenjem recipročnom vrijednošću intenziteta, imati će smisao suprotan smislu jedničnoga vektora pomoću kojeg je sila zadana:
|
|
|
|
1.30024656381632 1.30024656381632 |
Kutovi $\boldsymbol{\alpha}$, $\boldsymbol{\beta}$ i $\boldsymbol{\gamma}$ koje vektor sile zatvara s koordinatnim osima $x$, $y$ i $z$:
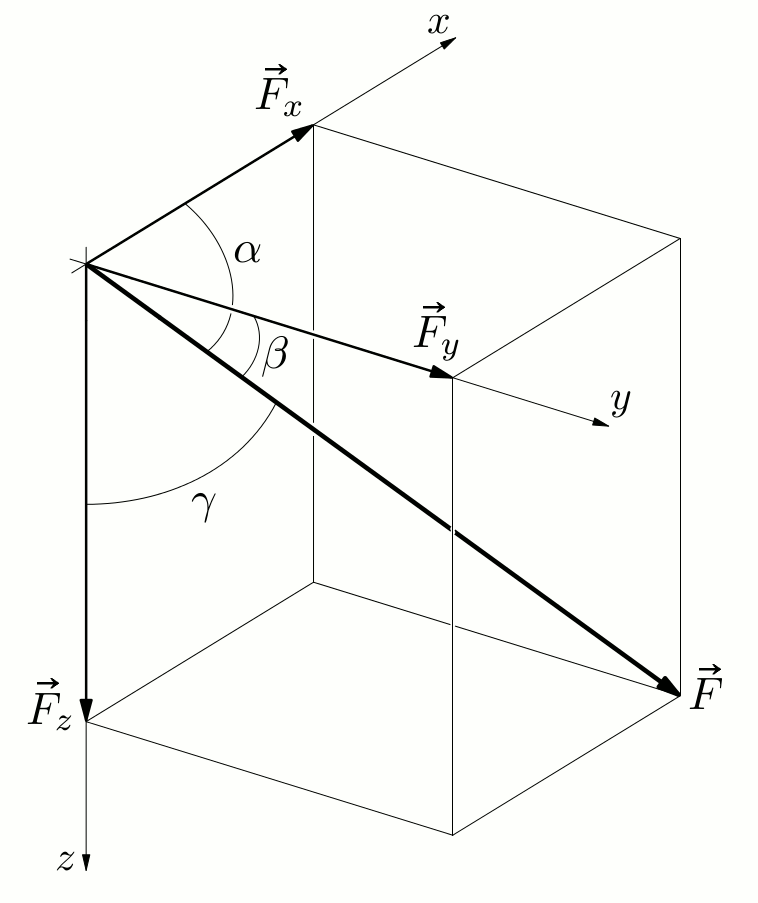
- iz $\vec{F}\cdot\vec{\imath}\:=\: \|\vec{F}\| \cdot \|\vec{\imath}\|\cdot\cos\,(\vec{F},\,\vec{\imath})$ slijedi
$\cos\alpha \;=\; \cos\,(\vec{F},\,\vec{\imath}) \;=\; \dfrac{\vec{F}\cdot \vec{\imath}}{\|\vec{F}\|} \;=\; \dfrac{F_x\,\vec{\imath} + F_y\,\vec{\jmath} + F_z\,\vec{k}}{\|\vec{F}\|}\cdot \vec{\imath}$
$\phantom{\cos\alpha} \;=\; \dfrac{F_x}{\|\vec{F}\|}\vec{\imath}\cdot\vec{\imath} + \dfrac{F_y}{\|\vec{F}\|}\vec{\jmath}\cdot\vec{\imath} + \dfrac{F_z}{\|\vec{F}\|}\vec{k}\cdot\vec{\imath} \;=\; \dfrac{F_x}{\|\vec{F}\|}\cdot 1 + \dfrac{F_y}{\|\vec{F}\|}\cdot 0 + \dfrac{F_z}{\|\vec{F}\|}\cdot 0 \;=\; \dfrac{F_x}{\|\vec{F}\|}$;
- na isti način dobivamo
$\cos\beta \,=\, \dfrac{F_y}{\|\vec{F}\|}$ i $\cos\gamma \,=\, \dfrac{F_z}{\|\vec{F}\|}$,
- pa su
$\alpha \:=\: \arccos \dfrac{F_x}{\|\vec{F}\|}$,
$\beta \:=\: \arccos \dfrac{F_y}{\|\vec{F}\|}$,
$\gamma \:=\: \arccos \dfrac{F_z}{\|\vec{F}\|}$;
- kutovi u radijanima:
|
|
|
|
|
|
1.30024656381632 1.30024656381632 |
- kutovi u stupnjevima $\left(\alpha\:[{}^\circ] \,=\, \dfrac{180}{\pi}\,\alpha\:[\mathrm{rad}]\right)$:
|
|
|
|
74.4986404330630 74.4986404330630 |
- kutovi $\alpha, \beta$ i $\gamma$ nisu međusobno neovisni: $\cos^2\alpha + \cos^2\beta +\cos^2\gamma = 1$
1 1 |
|
|
1 1 |
1.00000000000000 1.00000000000000 |
- usporedba s izrazom za jediničnu silu na pravcu i u smislu djelovanja sile $\vec{F}$ pokazuje da su skalarne komponente jedinične sile kosinusi kutova koje vektor sile zatvara s koordinatnim osima:
$\vec{f}_{\!0} \,=\, \dfrac{F_x}{\|\vec{F}\,\|} \vec{\imath} + \dfrac{F_y}{\|\vec{F}\,\|} \vec{\jmath} + \dfrac{F_z}{\|\vec{F}\,\|} \vec{k} \,=\, \cos\alpha\:\vec{\imath} + \cos\beta\:\vec{\jmath} + \cos\gamma\:\vec{k}$
Kutovi $\boldsymbol{\varphi}$ i $\boldsymbol{\psi}$ kojima je određen pravac i smisao djelovanja sile:
- $\varphi$ — kut između osi $x$ i vektora sile $\vec{F}_{x,y} = \vec{F}_x + \vec{F}_y$ (ortogonalne projekcije sile $\vec{F}$ na ravninu $xy$)
- $\psi$ — kut između vektora sile $\vec{F}_{x,y}$ i vektora sile $\vec{F}$

- $\varphi \;=\; \arccos\,\dfrac{\vec{\imath}\cdot(\vec{F}_x + \vec{F}_y)}{\|\vec{F}_x + \vec{F}_y\|} \;=\; \arccos\,\dfrac{F_x}{\|\vec{F}_x + \vec{F}_y\|}$
|
|
- $\psi \;=\; \arccos\,\dfrac{(\vec{F}_x + \vec{F}_y)\cdot\vec{F}}{\|\vec{F}_x + \vec{F}_y\|\cdot\|\vec{F}\|} \;=\; \arccos\,\dfrac{F_x^2 + F_y^2}{\|\vec{F}_x + \vec{F}_y\|\cdot\|\vec{F}\|} \;=\; \arccos\,\dfrac{\|\vec{F}_x + \vec{F}_y\|^2}{\|\vec{F}_x + \vec{F}_y\|\cdot\|\vec{F}\|} \;=\; \arccos\,\dfrac{\|\vec{F}_x + \vec{F}_y\|}{\|\vec{F}\|}$
|
|
|
|
|
|
56.3099324740202 47.9688862258027 56.3099324740202 47.9688862258027 |
Projiciranje sile na pravac
Ortogonalna projekcija sile $\vec{F}$ na pravac $p$ koji je zadan točkama $A$ i $B$:
- vrijednost projekcije (ili skalarna projekcija) jednaka je skalarnom produktu vektora sile i jediničnoga vektor $\vec{e}_p$ na pravcu $p$: $F_p = \vec{F}\cdot\vec{e}_p$
|
|
- jedinični vektor na pravcu, orijentiran od točke $A$ prema $B$: $\vec{e}_p = \dfrac{\vec{r}_B - \vec{r}_A}{\|\vec{r}_B - \vec{r}_A\|}$, gdje su $\vec{r}_A$ i $\vec{r}_B$ radijus-vektori točaka $A$ i $B$:
|
|
|
|
|
|
|
|
- ako se promijeni orijentacija jediničnoga vektora na pravcu, mijenja se predznak skalarne projekcije:
|
|
|
|
- predznak skalarne projekcije mijenja se i ako se promijeni smisao djelovanja sile:
|
|
|
|
- projekcija kao sila (ili vektorska projekcija) izračunava se množenjem skalarne projekcije i jediničnoga vektora na pravcu: $\vec{F}_p = (\vec{F}\cdot\vec{e}_p)\,\vec{e}_p$
|
|
(2, 2, 2) (2, 2, 2) |
|
|
- ako se promijeni orijentacija jediničnoga vektora na pravcu, orijentacija vektorske projekcije neće se promijeniti [objasnite zašto!]:
(2, 2, 2) (2, 2, 2) |
- promjenom orijetacije sile, međutim, mijenja se i orijentacija vektorske projekcije:
(-2, -2, -2) (-2, -2, -2) |
|
|
(-2, -2, -2) (-2, -2, -2) |
- ortogonalne projekcije sile na koordinatne osi jednake su njezinim ortogonalnim komponentama:
2 == 2 3 == 3 1 == 1 2 == 2 3 == 3 1 == 1 |
(2, 0, 0) == (2, 0, 0) (0, 3, 0) == (0, 3, 0) (0, 0, 1) == (0, 0, 1) (2, 0, 0) == (2, 0, 0) (0, 3, 0) == (0, 3, 0) (0, 0, 1) == (0, 0, 1) |
- općenitije, rastavi li se sila u vektorske komponente usporedne s međusobno okomitim pravcima, komponente će biti jednake ortogonalnim vektorskim projekcijama sile na te pravce (uz po volji odabrane orijentacije na njima); ako, međutim, pravci nisu međusobno okomiti, komponente neće biti jednake projekcijama (pokazat ćemo to u sljedećem primjeru).
Primjer 5.:
Rastavljanje sile u tri komponente usporedne s tri pravca koji nisu usporedni s jednom ravninom i od kojih po dva nisu međusobno usporedna
|
|
|
|
|
|
- za rastav vrijedi $\vec{F} \,=\, A\,\vec{a}_0 + B\:\vec{b}_0 + C\:\vec{c}_0$, pri čemu su $\vec{a}_0$, $\vec{b}_0$ i $\vec{c}_0$ jedinični vektori na pravcima $a$, $b$ i $c$ (njihova orijentacija nije bitna)
- korak 1.: jedinični vektori $\vec{a}_0$, $\vec{b}_0$ i $\vec{c}_0$:
(3.50000000000000, 0.325000000000000, 0.125000000000000) (0.425000000000000, 2.40000000000000, -0.250000000000000) (0.450000000000000, 0.375000000000000, 2.85000000000000) (3.50000000000000, 0.325000000000000, 0.125000000000000) (0.425000000000000, 2.40000000000000, -0.250000000000000) (0.450000000000000, 0.375000000000000, 2.85000000000000) |
(0.995087458577002, 0.0924009782964359, 0.0355388378063215) (0.173460357359315, 0.979540841558484, -0.102035504329009) (0.154661778667940, 0.128884815556617, 0.979524598230287) (0.995087458577002, 0.0924009782964359, 0.0355388378063215) (0.173460357359315, 0.979540841558484, -0.102035504329009) (0.154661778667940, 0.128884815556617, 0.979524598230287) |
- korak 2.: vrijednosti $A$, $B$ i $C$:
$\vec{F} \:= \vec{P} \quad \Longleftrightarrow \quad F_x = P_x \;\;\mathit\&\;\; F_y = P_y \;\;\mathit\&\;\;F_z = P_z$
$\begin{eqnarray} F_x\,\vec{\imath} + F_y\,\vec{\jmath} + F_z\,\vec{k} & \;= & A\,\vec{a}_0 + B\:\vec{b}_0 + C\:\vec{c}_0 \\ & \;= & A\,(a_{0,x}\,\vec{\imath} + a_{0,y}\,\vec{\jmath} + a_{0,z}\,\vec{k}) \,+\, B\,(b_{0,x}\,\vec{\imath} + b_{0,y}\,\vec{\jmath} + b_{0,z}\,\vec{k}) \,+\,C\,(c_{0,x}\,\vec{\imath} + c_{0,y}\,\vec{\jmath} + c_{0,z}\,\vec{k}) \\ & \;= & (A\,a_{0,x} + B\,b_{0,x} + C\,c_{0,x})\,\vec{\imath} + (A\,a_{0,y} + B\,b_{0,y} + C\,c_{0,y})\,\vec{\jmath} + (A\,a_{0,z} + B\,b_{0,z} + C\,c_{0,z})\,\vec{k} \end{eqnarray}$
$\!\!\left[\begin{array}{ccc} a_{0,x} & b_{0,x} & c_{0,x} \\ a_{0,y} & b_{0,y} & c_{0,y} \\ a_{0,z} & b_{0,z} & c_{0,z} \end{array}\right] \left[\begin{array}{c} A \\ B \\ C \end{array}\right] = \left[\begin{array}{c} F_x \\ F_y \\ F_z \end{array}\right] \qquad \Longrightarrow \qquad A, B,\, C$
[ 0.995087458577002 0.173460357359315 0.154661778667940] [0.0924009782964359 0.979540841558484 0.128884815556617] [0.0355388378063215 -0.102035504329009 0.979524598230287] [ 0.995087458577002 0.173460357359315 0.154661778667940] [0.0924009782964359 0.979540841558484 0.128884815556617] [0.0355388378063215 -0.102035504329009 0.979524598230287] |
0.967745631481687 0.779137335851645 2.11337940845003 0.967745631481687 0.779137335851645 2.11337940845003 |
- korak 3.: komponente $\vec{A} = A\,\vec{a}_0$, $\vec{B} = B\:\vec{b}_0$ i $\vec{C} = C\:\vec{c}_0$:
(0.962991540980108, 0.0894206430910100, 0.0343925550350039) (0.135149440708811, 0.763196841649756, -0.0794996710051829) (0.326859018311081, 0.272382515259234, 2.07010711597018) (0.962991540980108, 0.0894206430910100, 0.0343925550350039) (0.135149440708811, 0.763196841649756, -0.0794996710051829) (0.326859018311081, 0.272382515259234, 2.07010711597018) |
|
|
(1.42500000000000, 1.12500000000000, 2.02500000000000) (1.42500000000000, 1.12500000000000, 2.02500000000000) |
(1.42500000000000, 1.12500000000000, 2.02500000000000) (1.42500000000000, 1.12500000000000, 2.02500000000000) |
False False |
... da, ali ... prisjetite se: ispitivanje jednakosti pseudorealnih brojeva logičkim operatorom == gotovo nikad nije dobra zamisao;
umjesto toga,
- uzima se da su brojevi $a$ i $b$ jednaki ako je $|a - b| < \tau$, gdje je $\tau > 0$ odabrana točnost;
- uzima se da su vektori $\vec{u}$ i $\vec{v}$ jednaki ako je $\|\vec{v} - \vec{u}\| < \tau\,$;
stoga:
True True |
- promjena orijentacije vektora $\vec{a}_0$:
(-3.50000000000000, -0.325000000000000, -0.125000000000000) (0.425000000000000, 2.40000000000000, -0.250000000000000) (0.450000000000000, 0.375000000000000, 2.85000000000000) (-3.50000000000000, -0.325000000000000, -0.125000000000000) (0.425000000000000, 2.40000000000000, -0.250000000000000) (0.450000000000000, 0.375000000000000, 2.85000000000000) |
(-0.995087458577002, -0.0924009782964359, -0.0355388378063215) (0.173460357359315, 0.979540841558484, -0.102035504329009) (0.154661778667940, 0.128884815556617, 0.979524598230287) (-0.995087458577002, -0.0924009782964359, -0.0355388378063215) (0.173460357359315, 0.979540841558484, -0.102035504329009) (0.154661778667940, 0.128884815556617, 0.979524598230287) |
[ -0.995087458577002 0.173460357359315 0.154661778667940] [-0.0924009782964359 0.979540841558484 0.128884815556617] [-0.0355388378063215 -0.102035504329009 0.979524598230287] [ -0.995087458577002 0.173460357359315 0.154661778667940] [-0.0924009782964359 0.979540841558484 0.128884815556617] [-0.0355388378063215 -0.102035504329009 0.979524598230287] |
-0.967745631481687 0.779137335851645 2.11337940845003 -0.967745631481687 0.779137335851645 2.11337940845003 |
(0.962991540980108, 0.0894206430910100, 0.0343925550350039) (0.135149440708811, 0.763196841649756, -0.0794996710051829) (0.326859018311081, 0.272382515259234, 2.07010711597018) (0.962991540980108, 0.0894206430910100, 0.0343925550350039) (0.135149440708811, 0.763196841649756, -0.0794996710051829) (0.326859018311081, 0.272382515259234, 2.07010711597018) |
|
|
Ortogonalne projekcije sile na tri pravca:
(usporedbe radi, projekcije ćemo nacrtati na pravcima koji prolaze hvatištem sile, jer istom točkom prolaze i njezine komponente)
|
|
|
|
|
|
- budući da zadani pravci nisu međusobno okomiti, ortogonalne se projekcije na njih razlikuju od komponenata koje su s njima usporedne:
|
|
Sila u ravnini može se rastaviti u dvije komponente usporedne s dva pravca koji nisu međusobno usporedni; takav je rastav jedinstven. [Domaća zadaća: napravite primjer!]
|
|