PPPK_01 -- Sage

Programiranje postupaka proračuna konstrukcija

Ishodi učenja predmeta:

nakon uspješno svladanog predmeta moći ćete

razumjeti i objasniti strukturu programa za proračun konstrukcija,
razumjeti, objasniti i predvidjeti posljedice neizbježnih aproksimacija u numeričkom modeliranju konstrukcija i ograničene (konačne) točnosti numeričkih proračuna,
oblikovati i napisati jednostavniji računalni program,
izmijeniti, prilagoditi i dograditi složeniji računalni program za proračun konstrukcija, dostupan u izvornom kodu,
surađivati u timu ili s timom koji oblikuje i piše složeni računalni program za proračun konstrukcija.

SageMath (Sage) — otvoreni programski sustav za simboličku matematiku (Computer Algebra System, CAS)

Literatura:

Sage PREP Tutorials
M. O'Sullivan & D. Monarres: Sage Tutorial
G. Bard: Sage for Undergraduates
- color
- black & white
- appendix (plotting in color, complex functions and 3D graphics)
Sage Reference Manual (verzija na sage.grad.hr:1234)

Elementi programiranja

uz malo matematičke i numeričke analize

Zadatak

(*)

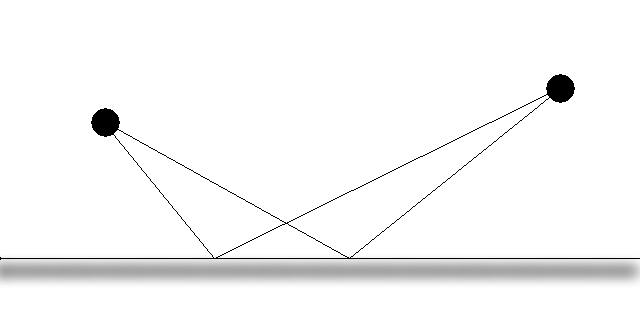
Treba odrediti minimum funkcije $L \ : \ x \ {\mapsto}\ \sqrt{{\left(x - x_{d}\right)}^{2} + y_{d}^{2}} + \sqrt{{\left(x - x_{v}\right)}^{2} + y_{v}^{2}}$.

var ('x_d y_d x_v y_v')

(x_d, y_d, x_v, y_v)

(x_d, y_d, x_v, y_v)

show (_)

$\newcommand{\Bold}[1]{\mathbf{#1}}\left(x_{d}, y_{d}, x_{v}, y_{v}\right)$

L (x) = sqrt ((x_v - x)^2 + y_v^2) + sqrt ((x_d - x)^2 + y_d^2)

show (L)

$\newcommand{\Bold}[1]{\mathbf{#1}}x \ {\mapsto}\ \sqrt{{\left(x - x_{d}\right)}^{2} + y_{d}^{2}} + \sqrt{{\left(x - x_{v}\right)}^{2} + y_{v}^{2}}$

xyd = (-1, 4)
xyv = (5, 1)

LL = L.subs (x_v = xyv[0], y_v = xyv[1], x_d = xyd[0], y_d = xyd[1])
show (LL)

$\newcommand{\Bold}[1]{\mathbf{#1}}x \ {\mapsto}\ \sqrt{{\left(x + 1\right)}^{2} + 16} + \sqrt{{\left(x - 5\right)}^{2} + 1}$

pl1 = plot (LL, -1, 6, aspect_ratio = 1)
pl1

pl2 = plot (LL, -16, 20, aspect_ratio = 1)
pl2

Matematička nas analiza uči da funkcija $L$ poprima minimum u točki $x$ u kojoj je, formalno, $L' (x) = 0$ ili, intuitivno–geometrijski, u točki u kojoj je tangenta na graf funkcije horizontalna, tako da funkcija u njoj ne raste niti ne pada. Dakle, ako je $f = L'$, za nalaženje minimuma treba riješiti nelinearnu jednadžbu $f(x) = 0$.

f = diff (L, x)
show (f)

$\newcommand{\Bold}[1]{\mathbf{#1}}x \ {\mapsto}\ \frac{x - x_{d}}{\sqrt{{\left(x - x_{d}\right)}^{2} + y_{d}^{2}}} + \frac{x - x_{v}}{\sqrt{{\left(x - x_{v}\right)}^{2} + y_{v}^{2}}}$

ff = diff (LL, x)
show (ff)

$\newcommand{\Bold}[1]{\mathbf{#1}}x \ {\mapsto}\ \frac{x + 1}{\sqrt{{\left(x + 1\right)}^{2} + 16}} + \frac{x - 5}{\sqrt{{\left(x - 5\right)}^{2} + 1}}$

ili

ff = f.subs (x_v = xyv[0], y_v = xyv[1], x_d = xyd[0], y_d = xyd[1]) 
show (ff)

$\newcommand{\Bold}[1]{\mathbf{#1}}x \ {\mapsto}\ \frac{x + 1}{\sqrt{{\left(x + 1\right)}^{2} + 16}} + \frac{x - 5}{\sqrt{{\left(x - 5\right)}^{2} + 1}}$

pf1 = plot (ff, -1, 6, aspect_ratio = 1, color = 'red')
pf1

pf2 = plot (ff, -16, 20, aspect_ratio = 2, color = 'red')
pf2

ord = parametric_plot ((19/5, x), (x, 0, LL (19/5)), linestyle = 'dotted', color = 'orange')

show (pl1 + pf1 + ord, aspect_ratio = 1, figsize = 9)

show (pl2 + pf2 + ord, aspect_ratio = 1, figsize = 7)

solve (ff(x) == 0, x)

[x == (5*sqrt(x^2 + 2*x + 17) - sqrt(x^2 - 10*x + 26))/(sqrt(x^2 + 2*x + 17) +
sqrt(x^2 - 10*x + 26))]

[x == (5*sqrt(x^2 + 2*x + 17) - sqrt(x^2 - 10*x + 26))/(sqrt(x^2 + 2*x + 17) + sqrt(x^2 - 10*x + 26))]

show (_[0])

$\newcommand{\Bold}[1]{\mathbf{#1}}x = \frac{5 \, \sqrt{x^{2} + 2 \, x + 17} - \sqrt{x^{2} - 10 \, x + 26}}{\sqrt{x^{2} + 2 \, x + 17} + \sqrt{x^{2} - 10 \, x + 26}}$

solve (ff(x) == 0, x, to_poly_solve = 'force' )

[x == (19/5)]

[x == (19/5)]

N ((_[0]).rhs())

3.80000000000000

3.80000000000000

Točno je rješenje $x \, = \, \dfrac{19}{5} \, = \, 3,\!8$.

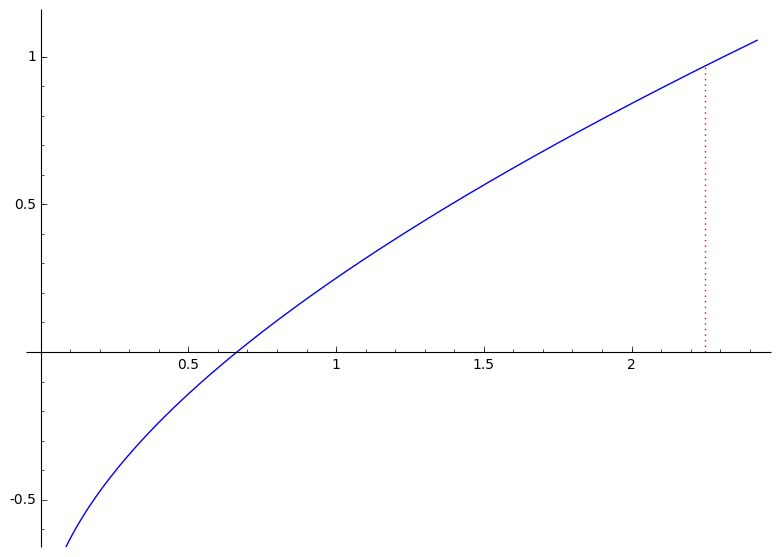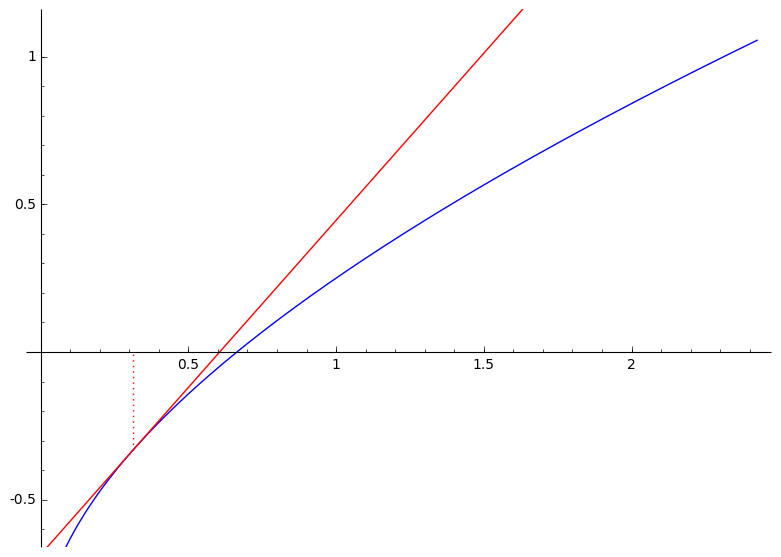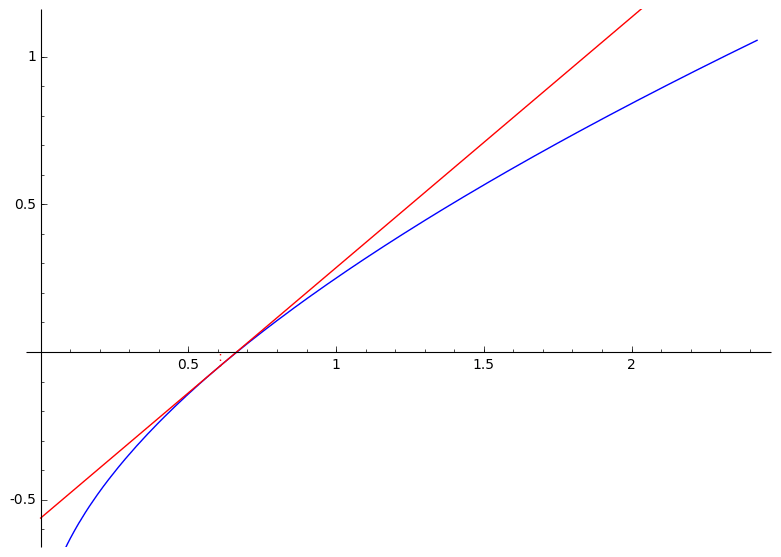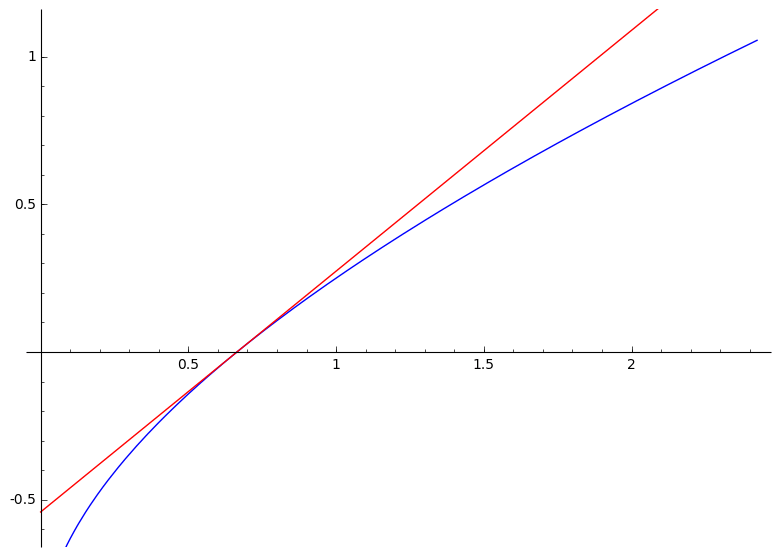
Newton–Raphsonov postupak rješavanja nelinearnih jednadžbi $\boldsymbol{f(x) = 0}$ (za neku drugu, „opću” funkciju $f$)

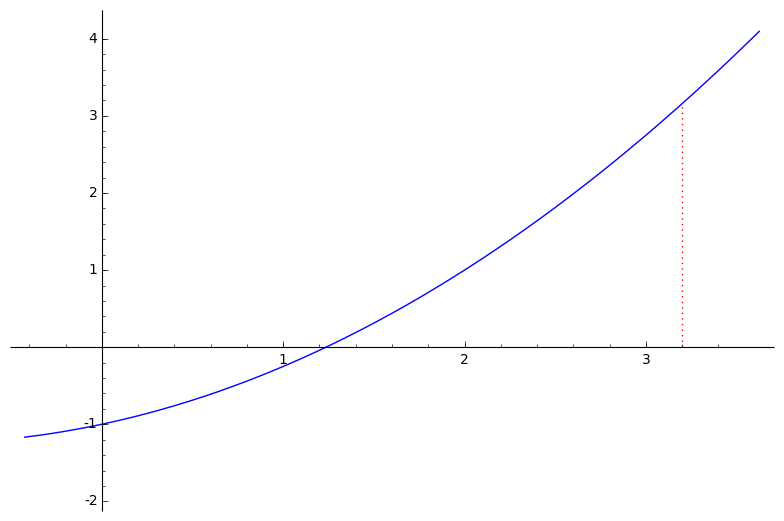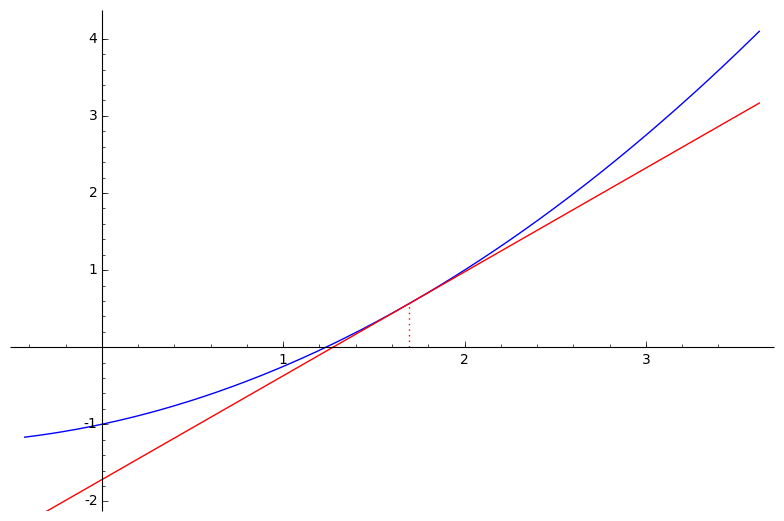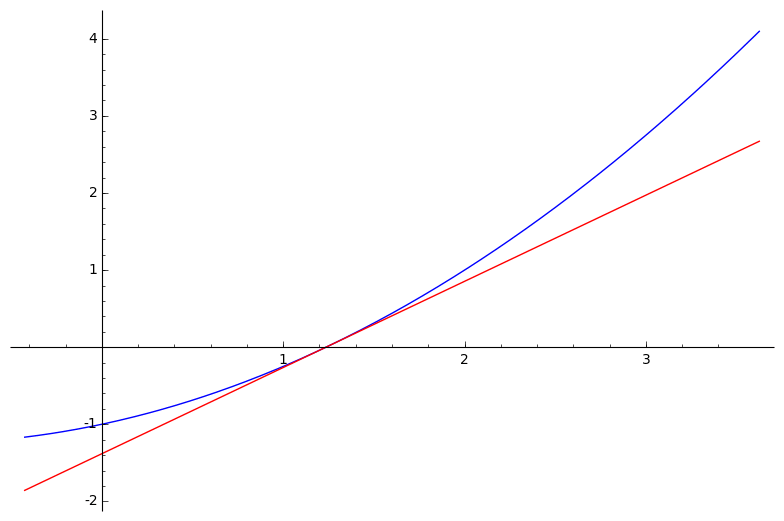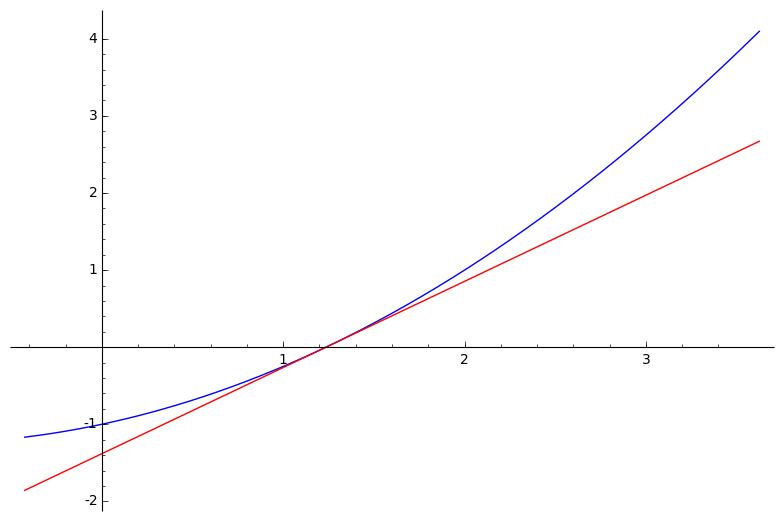
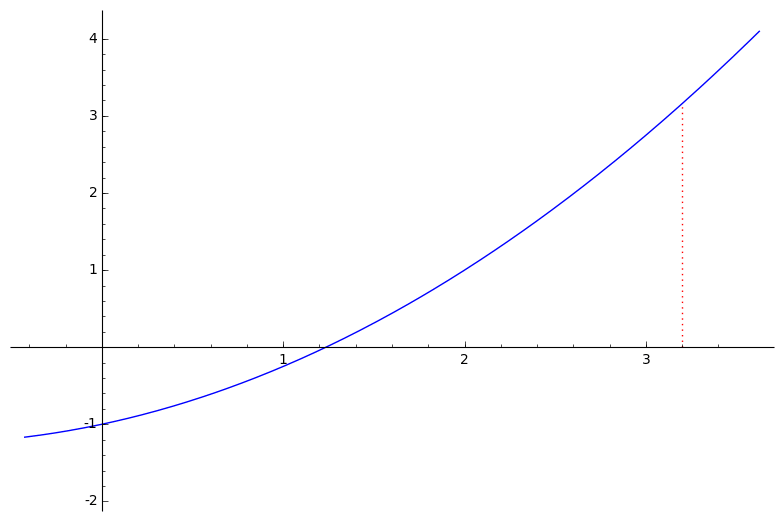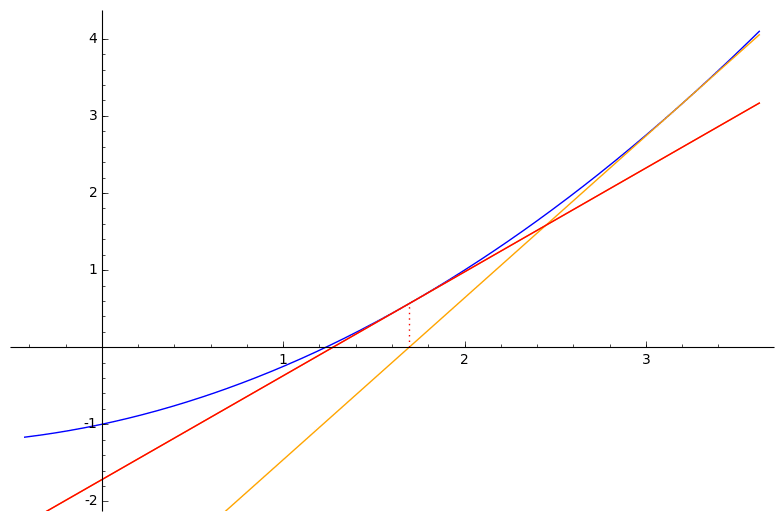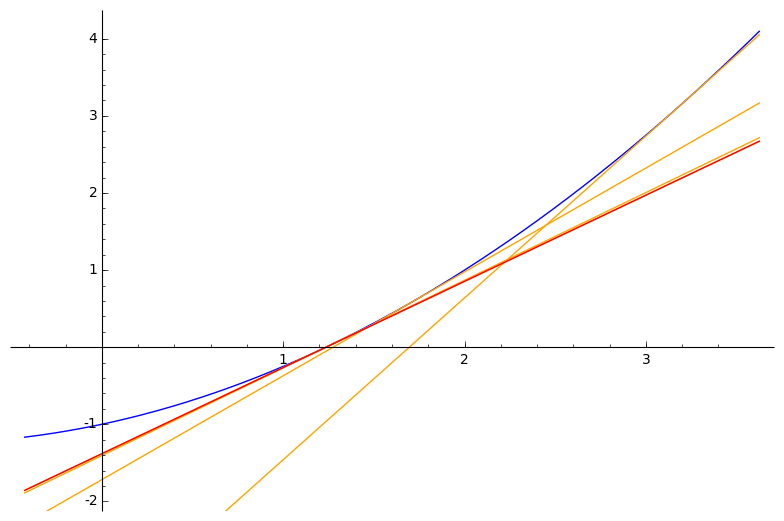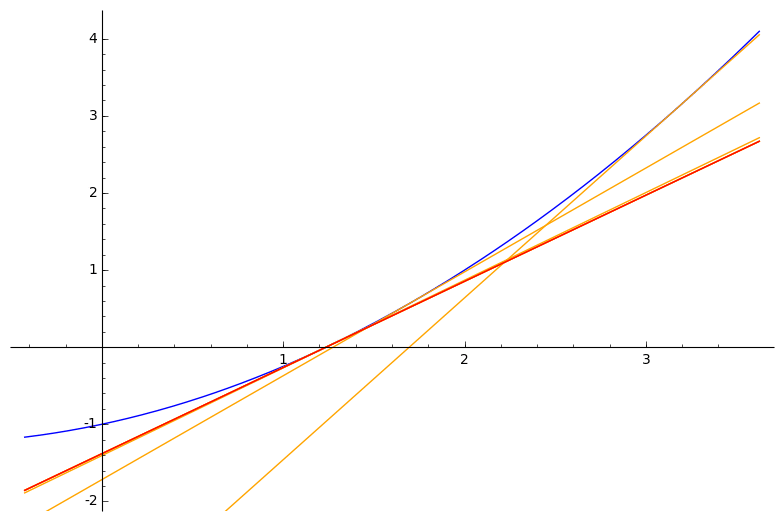
linearna aproksimacija funkcije $f$ u točki $x^{(k)}$:

$\bar{f}^{(k)}(x) \:=\: a\,x \,+\, b$

$a \:=\: f'\big(x^{(k)}\big)$

$\bar{f}^{(k)}\big(x^{(k)}\big) \:=\: a\,x^{(k)} \,+\, b \:=\: f\big(x^{(k)}\big) \qquad \Rightarrow \qquad f'\big(x^{(k)}\big)\: x^{(k)} \,+\, b \:=\: f\big(x^{(k)}\big) \qquad \Rightarrow \qquad b \:=\: f\big(x^{(k)}\big) \,-\, f'\big(x^{(k)}\big)\: x^{(k)} $

$\bar{f}^{(k)}(x) \:=\: f'\big(x^{(k)}\big)\: x\, +\, \big[ f\big(x^{(k)}\big) \,-\, f'\big(x^{(k)}\big) x^{(k)}\big]$

nultočka funkcije $\bar{f}^{(k)}$:

$f'\big(x^{(k)}\big)\: x\, +\, f\big(x^{(k)}\big) \,-\, f'\big(x^{(k)}\big) x^{(k)} \:=\: 0 \qquad \Rightarrow \qquad x \,=\, x^{(k)} - \dfrac{f\big(x^{(k)}\big)}{f'\big(x^{(k)}\big)}$

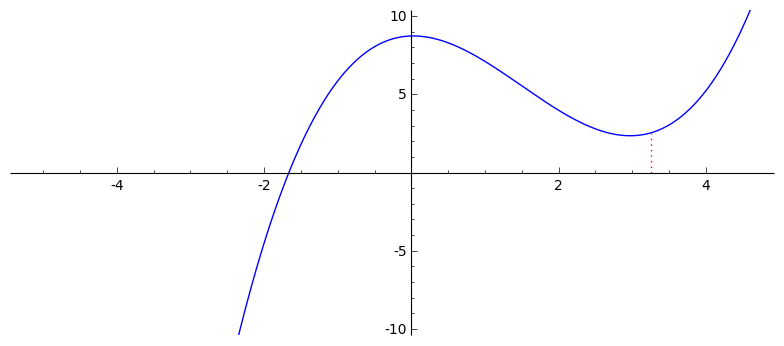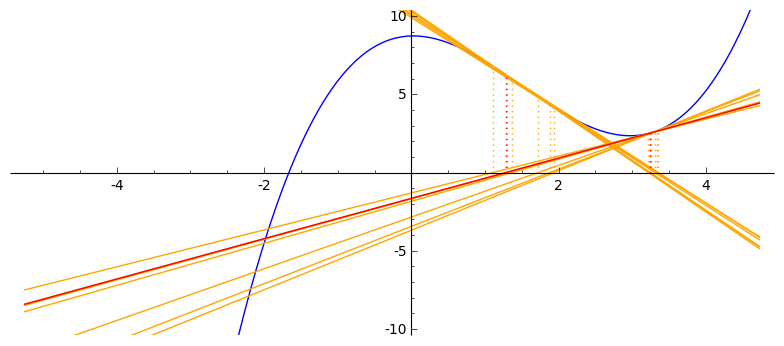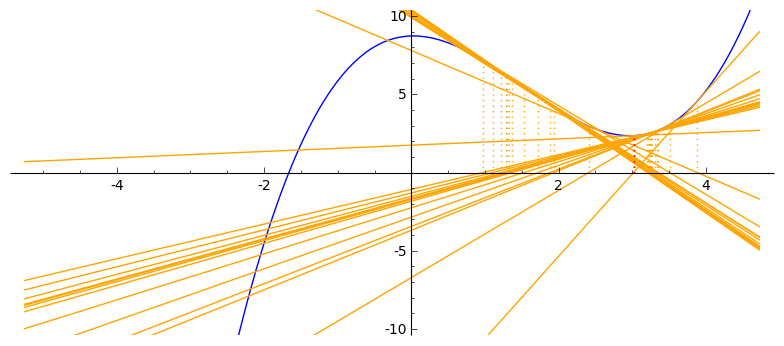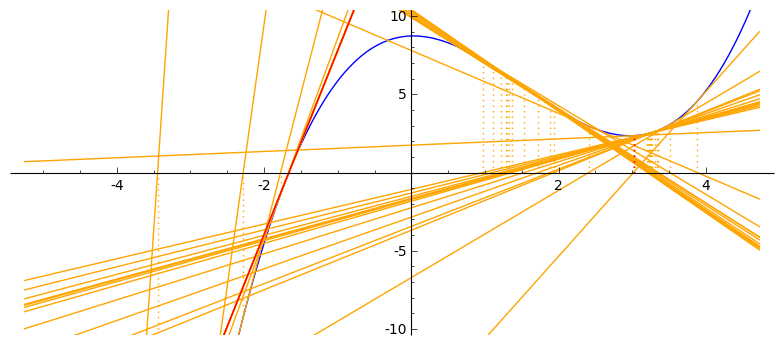
iteracija: $x^{(k+1)} \,=\, x^{(k)} - \dfrac{f\big(x^{(k)}\big)}{f'\big(x^{(k)}\big)}$

završetak iteracije: $\big|f\big(x^{(k)}\big)\big| < \tau_{f}$ ili $k > N$, gdje je $\tau_{f}$ odabrana točnost, a $N$ odabrani najveći broj koraka (za slučaj divergencije)

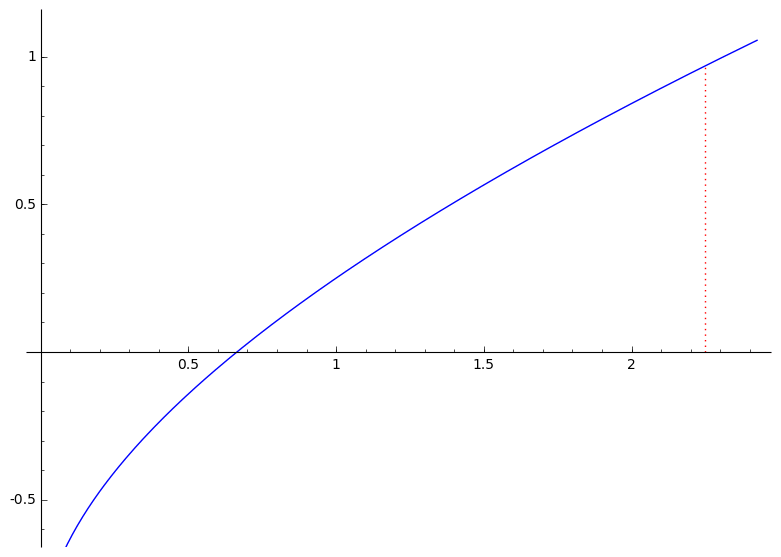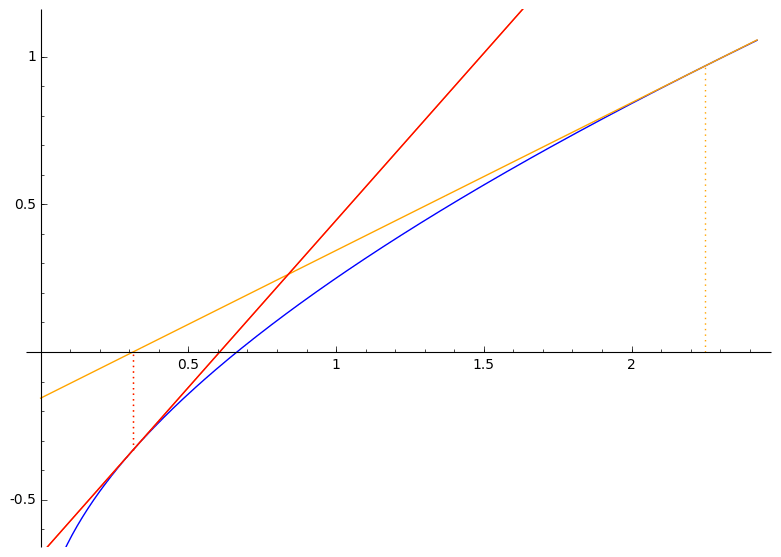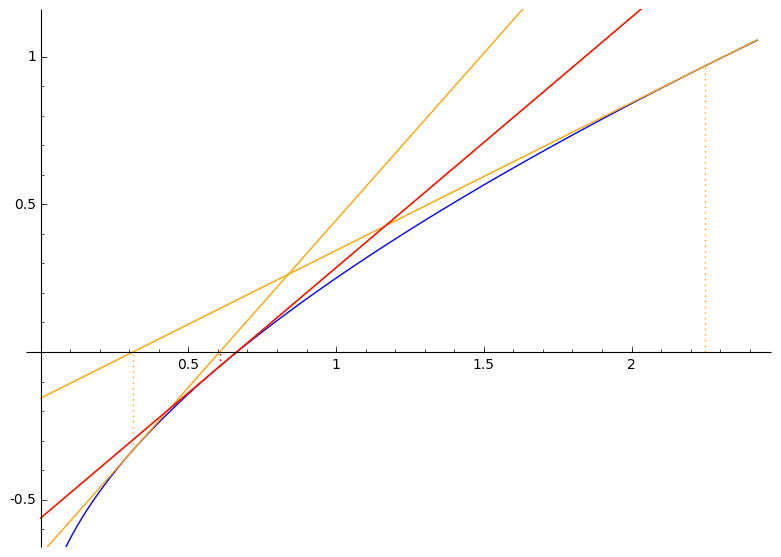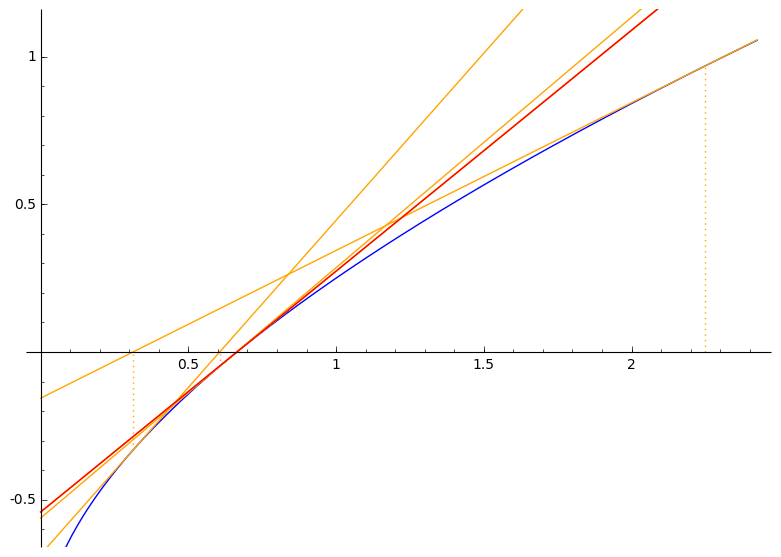
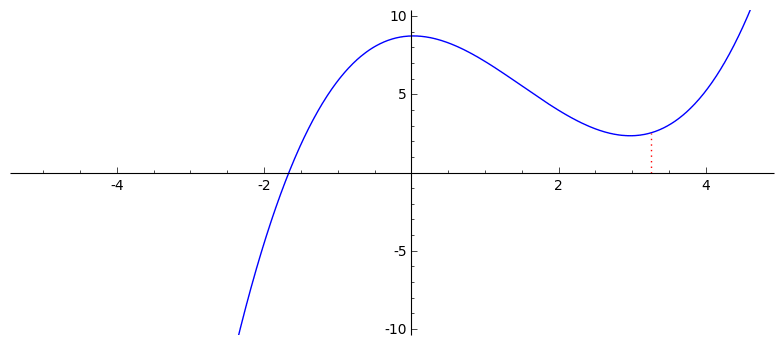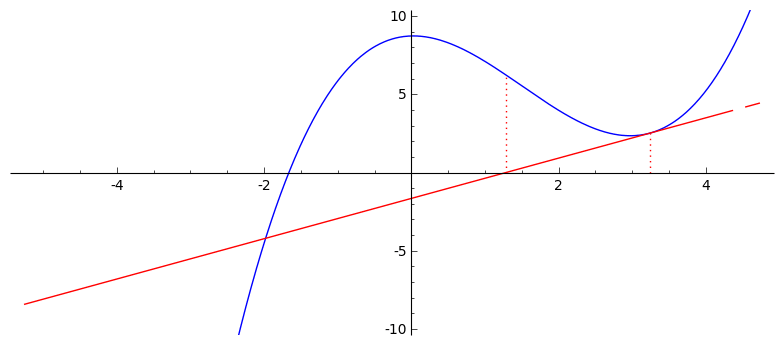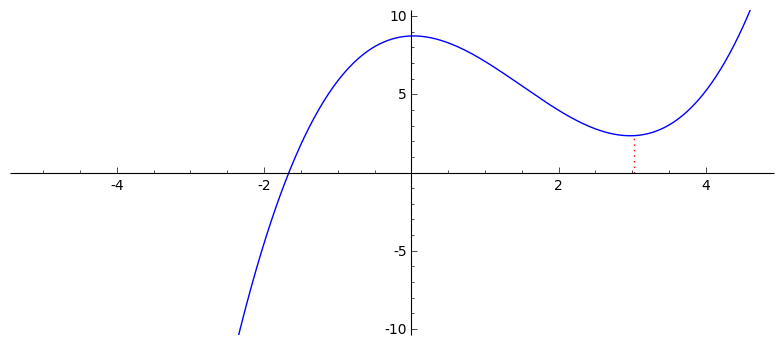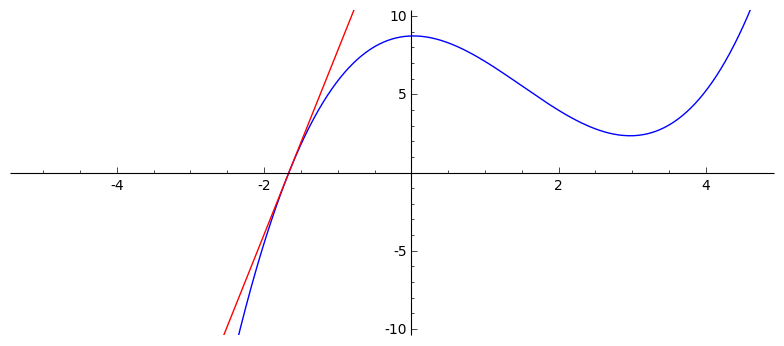
Još dva primjera:

df = diff (f, x)
show (df)

$\newcommand{\Bold}[1]{\mathbf{#1}}x \ {\mapsto}\ -\frac{{\left(x - x_{d}\right)}^{2}}{{\left({\left(x - x_{d}\right)}^{2} + y_{d}^{2}\right)}^{\frac{3}{2}}} - \frac{{\left(x - x_{v}\right)}^{2}}{{\left({\left(x - x_{v}\right)}^{2} + y_{v}^{2}\right)}^{\frac{3}{2}}} + \frac{1}{\sqrt{{\left(x - x_{d}\right)}^{2} + y_{d}^{2}}} + \frac{1}{\sqrt{{\left(x - x_{v}\right)}^{2} + y_{v}^{2}}}$

dff = diff (ff, x)
show (dff)

$\newcommand{\Bold}[1]{\mathbf{#1}}x \ {\mapsto}\ -\frac{{\left(x + 1\right)}^{2}}{{\left({\left(x + 1\right)}^{2} + 16\right)}^{\frac{3}{2}}} - \frac{{\left(x - 5\right)}^{2}}{{\left({\left(x - 5\right)}^{2} + 1\right)}^{\frac{3}{2}}} + \frac{1}{\sqrt{{\left(x + 1\right)}^{2} + 16}} + \frac{1}{\sqrt{{\left(x - 5\right)}^{2} + 1}}$

Programska funkcija definira se na sljedeći način:

def naziv (parametri) :

tijelo funkcije

Definicija funkcije započinje ključnom riječju def iza koje slijedi naziv funkcije. Dobro odabrani naziv trebao bi biti ključem značenja i svrhe funkcije. Nakon naziva se između okruglih zagrada navode parametri funkcije. Parametri su varijable koje pri upotrebi funkcije prihvaćaju vrijednosti koje se prenose u funkciju — koje „ulaze” u nju. (Par zagrada treba napisati i ako funkcija nema parametara.) Prvi redak definicije funkcije, koji se naziva i zaglavljem funkcije, završava dvotočkom.

Tijelo funkcije je niz naredaba koje propisuju kako funkcija radi ono čemu je namijenjena. Tijelo je programska realizacija algoritma.

Algoritam je razgovijetan, potpun i nedvosmislen opis postupka rješavanja određenoga zadatka u obliku niza jasno definiranih koraka. Svaki algoritam mora imati sljedeća svojstva:

konačnost — izvođenje algoritma, neovisno o konkretnom skupu ulaznih/početnih podataka, mora završiti u konačnom broju koraka;
jedinstveni početak — svako izvođenje algoritma mora početi istim korakom;
jedinstveni nastavak — iza svakoga pojedinog koraka mora slijediti jednoznačno određeni korak;
rješenje — svako izvođenje algoritma mora dovesti do rješenja ili završiti s naznakom da za zadani skup početnih podataka zadatak nije rješiv tim algoritmom.

Vrijednost koju funkcija izračunava i „vraća” naredbom return je vrijednost funkcije.

Upotreba funkcije naziva se i pozivom funkcije:

naziv (argumenti)

Nakon naziva se između okruglih zagrada navode funkcijski argumenti — vrijednosti koje se prenose u funkciju pridruživanjem parametrima. (Argumenti se katkad nazivaju aktualnim parametrima, dok se za parametre tada upotrebljava naziv formalni parametri.)

show (ff)

$\newcommand{\Bold}[1]{\mathbf{#1}}x \ {\mapsto}\ \frac{x + 1}{\sqrt{{\left(x + 1\right)}^{2} + 16}} + \frac{x - 5}{\sqrt{{\left(x - 5\right)}^{2} + 1}}$

def fp (x) : 
    return (x + 1)/sqrt((x + 1)^2 + 16) + (x - 5)/sqrt((x - 5)^2 + 1)

fp (5.)

0.832050294337844

0.832050294337844

show (dff)

def dfp (x) : 
    x1 = x + 1
    x5 = x - 5
    r = -x1^2/(x1^2 + 16)^(3/2) - x5^2/(x5^2 + 1)^(3/2) 
    r += 1/sqrt(x1^2 + 16) + 1/sqrt(x5^2 + 1)
    return r

dfp (5.)

1.04266924586348

1.04266924586348

Newton–Raphsonov postupak:

$x^{(0)} \,=\, \text{na neki način (primjerice bacanjem kocaka) pretpostavljeni broj}$

$x^{(k+1)} \,=\, x^{(k)} - \dfrac{f\big(x^{(k)}\big)}{f'\big(x^{(k)}\big)}$

dok su $\big|f\big(x^{(k)}\big)\big| > \tau_{f}$ i $k < N$ (oba uvjeta moraju biti zadovoljena)

Prva verzija programske funkcije newton_raphson():

def newton_raphson (f, df, x0, tol_f, max_iter) :
    xk = x0
    
    for k in xrange (max_iter) : 
        fk = f (xk)
        if abs (fk) < tol_f :
            break 
        dfk = df (xk) 
        xk = xk - fk/dfk
        
    return xk

newton_raphson (fp, dfp, 5., 1e-7, 100)

3.80000000004635

3.80000000004635

fp (_)

1.52002854747479e-11

1.52002854747479e-11

newton_raphson (fp, dfp, 7., 1e-7, 100)

NaN + NaN*I

NaN + NaN*I

def newton_raphson_listing (f, df, x0, tol_f, max_iter) :
    # prva verzija, ali s ispisom
    
    xk = x0
    
    for k in xrange (max_iter) : 
        fk = f (xk)
        if abs (fk) < tol_f :
            break 
        dfk = df (xk)
        print k, '  ', xk, '  ', fk, '  ', dfk
        xk = xk - fk/dfk

    print k, '  ', xk, '  ', fk        
    return xk

newton_raphson_listing (fp, dfp, 5., 1e-7, 100)

0    5.00000000000000    0.832050294337844    1.04266924586348
1    4.20199977352474    0.168995782368261    0.534158108945978
2    3.88562194542862    0.0294799921364655    0.361472597627328
3    3.80406668417239    0.00133673130512302    0.329444455848224
4    3.80000915252663    3.00170821554424e-6    0.327966641072566
5    3.80000000004635    1.52002854747479e-11
3.80000000004635

0    5.00000000000000    0.832050294337844    1.04266924586348
1    4.20199977352474    0.168995782368261    0.534158108945978
2    3.88562194542862    0.0294799921364655    0.361472597627328
3    3.80406668417239    0.00133673130512302    0.329444455848224
4    3.80000915252663    3.00170821554424e-6    0.327966641072566
5    3.80000000004635    1.52002854747479e-11
3.80000000004635

newton_raphson_listing (fp, dfp, 7., 1e-7, 10)

0    7.00000000000000    1.78885438199983    0.111803398874990
1    -8.99999999999999    -1.89188589083065    0.0227223399272208
2    74.2610504415619    1.99848639858029    0.0000403829985181937
3    -49414.0501674566    -1.99999999651880    1.40901172836477e-13
4    1.41943459326446e13    2.00000000000000    0.000000000000000
5    -infinity    NaN    NaN
6    NaN    NaN + NaN*I    NaN + NaN*I
7    NaN + NaN*I    NaN + NaN*I    NaN + NaN*I
8    NaN + NaN*I    NaN + NaN*I    NaN + NaN*I
9    NaN + NaN*I    NaN + NaN*I    NaN + NaN*I
9    NaN + NaN*I    NaN + NaN*I
NaN + NaN*I

0    7.00000000000000    1.78885438199983    0.111803398874990
1    -8.99999999999999    -1.89188589083065    0.0227223399272208
2    74.2610504415619    1.99848639858029    0.0000403829985181937
3    -49414.0501674566    -1.99999999651880    1.40901172836477e-13
4    1.41943459326446e13    2.00000000000000    0.000000000000000
5    -infinity    NaN    NaN
6    NaN    NaN + NaN*I    NaN + NaN*I
7    NaN + NaN*I    NaN + NaN*I    NaN + NaN*I
8    NaN + NaN*I    NaN + NaN*I    NaN + NaN*I
9    NaN + NaN*I    NaN + NaN*I    NaN + NaN*I
9    NaN + NaN*I    NaN + NaN*I
NaN + NaN*I

show (ff)

$\newcommand{\Bold}[1]{\mathbf{#1}}x \ {\mapsto}\ \frac{x + 1}{\sqrt{{\left(x + 1\right)}^{2} + 16}} + \frac{x - 5}{\sqrt{{\left(x - 5\right)}^{2} + 1}}$

pf2

xyd; xyv

(-1, 4)
(5, 1)

(-1, 4)
(5, 1)

... u rješavanju nelinearnoga zadatka korisno je poznavati ga i razumjeti

Druga verzija:

def newton_raphson (f, df, x0, tol_f, tol_df, max_iter) :
    xk = x0
    
    for k in xrange (max_iter) : 
        fk = f (xk)
        if abs (fk) < tol_f :
            break 
        dfk = df (xk) 
        if abs (dfk) < tol_df :
            break 
        xk = xk - fk/dfk
        
    return xk

newton_raphson (fp, dfp, 5., 1e-7, 1e-7, 100)

3.80000000004635

3.80000000004635

newton_raphson (fp, dfp, 7., 1e-7, 1e-7, 100)

-49414.0501674566

-49414.0501674566

fp (_)

-1.99999999651880

-1.99999999651880

def newton_raphson (f, df, x0, tol_f = 1e-5, tol_df = 1e-5, max_iter = 100) :
    xk = x0
    
    for k in xrange (max_iter) : 
        fk = f (xk)
        if abs (fk) < tol_f :
            break 
        dfk = df (xk) 
        if abs (dfk) < tol_df :
            xk = oo
            break 
        xk = xk - fk/dfk
    
    if k + 1 == max_iter :
        print "Warning: maximal number of steps reached:", max_iter
            
    return xk, k + 1

newton_raphson (fp, dfp, 5.)

(3.80000915252663, 5)

(3.80000915252663, 5)

newton_raphson (fp, dfp, 7.)

(+Infinity, 4)

(+Infinity, 4)

newton_raphson (fp, dfp, 5., 1e-7, max_iter = 3)

Warning: maximal number of steps reached: 3
(3.80406668417239, 3)

Warning: maximal number of steps reached: 3
(3.80406668417239, 3)

xx, st = newton_raphson (fp, dfp, 5., 1e-7)
xx; fp (xx)

3.80000000004635
1.52002854747479e-11

3.80000000004635
1.52002854747479e-11

Konačna verzija:

def newton_raphson (f, df, x0, tol_f = 1e-5, tol_df = None, max_iter = 100, n_steps = False, prn = False) : 
    xk = x0
    if tol_df == None :
        tol_df = tol_f
    
    for k in xrange (max_iter) :
        fk = f (xk)
        if prn :
            print 'step =', k, '  x =', xk, '  f(x) =', fk
        if abs (fk) < tol_f : 
            break 
        dfk = df (xk)
        if abs (dfk) < tol_df : 
            xk = oo
            print "Tangent slope f'(x) =", dfk, " < ", tol_df
            break 
        xk -= fk / dfk
    
    if k + 1 == max_iter :
        print "Warning: maximal number of steps reached:", max_iter
            
    if n_steps == False :
        return xk
    else :
        return xk, k + 1

xx = newton_raphson (fp, dfp, 5.)
xx

3.80000915252663

3.80000915252663

fp (xx)

3.00170821554424e-6

3.00170821554424e-6

xx = newton_raphson (fp, dfp, 5., n_steps = True)
xx

(3.80000915252663, 5)

(3.80000915252663, 5)

fp (xx)

Traceback (click to the left of this block for traceback)
...
TypeError: unsupported operand parent(s) for +: '<type 'tuple'>' and
'Integer Ring'

Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
  File "_sage_input_59.py", line 10, in <module>
    exec compile(u'open("___code___.py","w").write("# -*- coding: utf-8 -*-\\n" + _support_.preparse_worksheet_cell(base64.b64decode("ZnAgKHh4KQ=="),globals())+"\\n"); execfile(os.path.abspath("___code___.py"))
  File "", line 1, in <module>
    
  File "/tmp/tmpe1ew72/___code___.py", line 2, in <module>
    exec compile(u'fp (xx)
  File "", line 1, in <module>
    
  File "/tmp/tmpRn9J7H/___code___.py", line 4, in fp
    return (x + _sage_const_1 )/sqrt((x + _sage_const_1 )**_sage_const_2  + _sage_const_16 ) + (x - _sage_const_5 )/sqrt((x - _sage_const_5 )**_sage_const_2  + _sage_const_1 )
  File "sage/rings/integer.pyx", line 1792, in sage.rings.integer.Integer.__add__ (build/cythonized/sage/rings/integer.c:12197)
  File "sage/structure/coerce.pyx", line 1207, in sage.structure.coerce.CoercionModel.bin_op (build/cythonized/sage/structure/coerce.c:10896)
TypeError: unsupported operand parent(s) for +: '<type 'tuple'>' and 'Integer Ring'

fp (xx[0])

3.00170821554424e-6

3.00170821554424e-6

xx, st = newton_raphson (fp, dfp, 5., tol_f = 1.e-7, n_steps = True)
xx; st

3.80000000004635
6

3.80000000004635
6

fp (xx)

1.52002854747479e-11

1.52002854747479e-11

xx, st = newton_raphson (fp, dfp, 5., tol_f = 1.e-7)

Traceback (click to the left of this block for traceback)
...
TypeError: 'sage.rings.real_mpfr.RealNumber' object is not iterable

Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
  File "_sage_input_63.py", line 10, in <module>
    exec compile(u'open("___code___.py","w").write("# -*- coding: utf-8 -*-\\n" + _support_.preparse_worksheet_cell(base64.b64decode("eHgsIHN0ID0gbmV3dG9uX3JhcGhzb24gKGZwLCBkZnAsIDUuLCB0b2xfZiA9IDEuZS03KQ=="),globals())+"\\n"); execfile(os.path.abspath("___code___.py"))
  File "", line 1, in <module>
    
  File "/tmp/tmpYk2ycc/___code___.py", line 3, in <module>
    exec compile(u'xx, st = newton_raphson (fp, dfp, _sage_const_5p , tol_f = _sage_const_1pen7 )
  File "", line 1, in <module>
    
TypeError: 'sage.rings.real_mpfr.RealNumber' object is not iterable

xx = newton_raphson (fp, dfp, 5., tol_f = 1.e-7)
xx

3.80000000004635

3.80000000004635

xx = newton_raphson (fp, dfp, 5., tol_f = 1.e-13, prn = True)

step = 0   x = 5.00000000000000   f(x) = 0.832050294337844
step = 1   x = 4.20199977352474   f(x) = 0.168995782368261
step = 2   x = 3.88562194542862   f(x) = 0.0294799921364655
step = 3   x = 3.80406668417239   f(x) = 0.00133673130512302
step = 4   x = 3.80000915252663   f(x) = 3.00170821554424e-6
step = 5   x = 3.80000000004635   f(x) = 1.52002854747479e-11
step = 6   x = 3.80000000000000   f(x) = 0.000000000000000

step = 0   x = 5.00000000000000   f(x) = 0.832050294337844
step = 1   x = 4.20199977352474   f(x) = 0.168995782368261
step = 2   x = 3.88562194542862   f(x) = 0.0294799921364655
step = 3   x = 3.80406668417239   f(x) = 0.00133673130512302
step = 4   x = 3.80000915252663   f(x) = 3.00170821554424e-6
step = 5   x = 3.80000000004635   f(x) = 1.52002854747479e-11
step = 6   x = 3.80000000000000   f(x) = 0.000000000000000

newton_raphson (fp, dfp, 5., tol_f = 1.e-9, max_iter = 4, prn = True)

step = 0   x = 5.00000000000000   f(x) = 0.832050294337844
step = 1   x = 4.20199977352474   f(x) = 0.168995782368261
step = 2   x = 3.88562194542862   f(x) = 0.0294799921364655
step = 3   x = 3.80406668417239   f(x) = 0.00133673130512302
Warning: maximal number of steps reached: 4
3.80000915252663

step = 0   x = 5.00000000000000   f(x) = 0.832050294337844
step = 1   x = 4.20199977352474   f(x) = 0.168995782368261
step = 2   x = 3.88562194542862   f(x) = 0.0294799921364655
step = 3   x = 3.80406668417239   f(x) = 0.00133673130512302
Warning: maximal number of steps reached: 4
3.80000915252663

xx = newton_raphson (fp, dfp, 3.789, tol_f = 1.e-7, prn = True)
xx; fp (xx)

step = 0   x = 3.78900000000000   f(x) = -0.00358578168341916
step = 1   x = 3.80006689346948   f(x) = 0.0000219394162994657
step = 2   x = 3.80000000247579   f(x) = 8.11967382219336e-10
3.80000000247579
8.11967382219336e-10

step = 0   x = 3.78900000000000   f(x) = -0.00358578168341916
step = 1   x = 3.80006689346948   f(x) = 0.0000219394162994657
step = 2   x = 3.80000000247579   f(x) = 8.11967382219336e-10
3.80000000247579
8.11967382219336e-10

xx = newton_raphson (fp, dfp, 0., tol_f = 1.e-9, n_steps = True)
xx[0]; fp (xx[0]); xx[1]

3.80000000000000
0.000000000000000
7

3.80000000000000
0.000000000000000
7

newton_raphson (fp, dfp, 6.6, tol_f = 1.e-7)

3.80000000010167

3.80000000010167

newton_raphson (fp, dfp, 6.7, tol_f = 1.e-7)

Tangent slope f'(x) = 1.04436621297613e-16  <  1.00000000000000e-7
+Infinity

Tangent slope f'(x) = 1.04436621297613e-16  <  1.00000000000000e-7
+Infinity

newton_raphson (fp, dfp, 6.618, tol_f = 1.e-7)

Tangent slope f'(x) = 1.73422661322621e-12  <  1.00000000000000e-7
+Infinity

Tangent slope f'(x) = 1.73422661322621e-12  <  1.00000000000000e-7
+Infinity

newton_raphson (fp, dfp, 6.61797, tol_f = 1.e-7)

3.80000006304201

3.80000006304201

newton_raphson (fp, dfp, 6.61798, tol_f = 1.e-7)

Tangent slope f'(x) = 3.77016804277777e-14  <  1.00000000000000e-7
+Infinity

Tangent slope f'(x) = 3.77016804277777e-14  <  1.00000000000000e-7
+Infinity

Jedno poopćenje:

show (f)

$\newcommand{\Bold}[1]{\mathbf{#1}}x \ {\mapsto}\ \frac{x - x_{d}}{\sqrt{{\left(x - x_{d}\right)}^{2} + y_{d}^{2}}} + \frac{x - x_{v}}{\sqrt{{\left(x - x_{v}\right)}^{2} + y_{v}^{2}}}$

show (ff)

$\newcommand{\Bold}[1]{\mathbf{#1}}x \ {\mapsto}\ \frac{x + 1}{\sqrt{{\left(x + 1\right)}^{2} + 16}} + \frac{x - 5}{\sqrt{{\left(x - 5\right)}^{2} + 1}}$

def gp (x, dq, vj) :
    (xd, yd) = dq
    (xv, yv) = vj
    xxd = x - xd
    xxv = x - xv
    return xxd/sqrt(xxd^2 + yd^2) + xxv/sqrt(xxv^2 + yv^2)

xyd; xyv

(-1, 4)
(5, 1)

(-1, 4)
(5, 1)

fp (5.); gp (5., xyd, xyv)

0.832050294337844
0.832050294337844

0.832050294337844
0.832050294337844

show (df)

def dgp (x, dq, vj) : 
    (xd, yd) = dq
    (xv, yv) = vj
    xxd = x - xd
    xxv = x - xv
    r = -xxd^2/(xxd^2 + yd^2)^(3/2) - xxv^2/(xxv^2 + yv^2)^(3/2) 
    r += 1/sqrt(xxd^2 + yd^2) + 1/sqrt(xxv^2 + yv^2)
    return r

newton_raphson (gp, dgp, 5.)

Traceback (click to the left of this block for traceback)
...
TypeError: gp() takes exactly 3 arguments (1 given)

Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
  File "_sage_input_81.py", line 10, in <module>
    exec compile(u'open("___code___.py","w").write("# -*- coding: utf-8 -*-\\n" + _support_.preparse_worksheet_cell(base64.b64decode("bmV3dG9uX3JhcGhzb24gKGdwLCBkZ3AsIDUuKQ=="),globals())+"\\n"); execfile(os.path.abspath("___code___.py"))
  File "", line 1, in <module>
    
  File "/tmp/tmpfrMX8w/___code___.py", line 3, in <module>
    exec compile(u'newton_raphson (gp, dgp, _sage_const_5p )
  File "", line 1, in <module>
    
  File "/tmp/tmpQlTEPJ/___code___.py", line 9, in newton_raphson
    fk = f (xk)
TypeError: gp() takes exactly 3 arguments (1 given)

newton_raphson (gp, dgp, 5., xyd, xyv)

Traceback (click to the left of this block for traceback)
...
TypeError: gp() takes exactly 3 arguments (1 given)

Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
  File "_sage_input_82.py", line 10, in <module>
    exec compile(u'open("___code___.py","w").write("# -*- coding: utf-8 -*-\\n" + _support_.preparse_worksheet_cell(base64.b64decode("bmV3dG9uX3JhcGhzb24gKGdwLCBkZ3AsIDUuLCB4eWQsIHh5dik="),globals())+"\\n"); execfile(os.path.abspath("___code___.py"))
  File "", line 1, in <module>
    
  File "/tmp/tmpvnTklM/___code___.py", line 3, in <module>
    exec compile(u'newton_raphson (gp, dgp, _sage_const_5p , xyd, xyv)
  File "", line 1, in <module>
    
  File "/tmp/tmpQlTEPJ/___code___.py", line 9, in newton_raphson
    fk = f (xk)
TypeError: gp() takes exactly 3 arguments (1 given)

def bind_2nd (f, *a) :
    def f_ (x) :
        return f (x, *a)
    return f_

gp1 = bind_2nd (gp, xyd, xyv)
gp1 (5.)

0.832050294337844

0.832050294337844

gp1

<function f_ at 0x7f562dbd0c08>

<function f_ at 0x7f562dbd0c08>

bind_2nd (gp, xyd, xyv)

<function f_ at 0x7f562dbd0b18>

<function f_ at 0x7f562dbd0b18>

bind_2nd (gp, xyd, xyv) (5.)

0.832050294337844

0.832050294337844

def bind_2nd (f, *a) :
    return lambda x : f (x, *a)

bind_2nd (gp, xyd, xyv)

<function <lambda> at 0x7f562de13668>

<function <lambda> at 0x7f562de13668>

bind_2nd (gp, xyd, xyv) (5.)

0.832050294337844

0.832050294337844

newton_raphson (bind_2nd (gp, xyd, xyv), bind_2nd (dgp, xyd, xyv), 5.)

3.80000915252663

3.80000915252663

Minimizacija primjenom Newton-Raphsonova postupka:

def min_nr (F, x0, tolf = 1.e-5, toldf = None, max_iter = 100, n_steps = False, prn = False) :
    f = diff (F, x)
    df = diff (f, x)
    xm = newton_raphson (f, df, x0, tolf, toldf, max_iter, n_steps, prn)
    return xm

xmin = min_nr (LL, 6., tolf = 1.e-7, prn = True)
fmin = LL (xmin)
xmin; fmin

step = 0   x = 6.00000000000000   f(x) = 1.57534992331101
step = 1   x = 1.89843432768716   f(x) = -0.364994091915365
step = 2   x = 4.15652661816414   f(x) = 0.145393647790519
step = 3   x = 3.86816299760975   f(x) = 0.0232325785022762
step = 4   x = 3.80257728615178   f(x) = 0.000846462445067031
step = 5   x = 3.80000367572973   f(x) = 1.20550697590982e-6
step = 6   x = 3.80000000000748   f(x) = 2.45159448297727e-12
3.80000000000748
7.81024967590665

step = 0   x = 6.00000000000000   f(x) = 1.57534992331101
step = 1   x = 1.89843432768716   f(x) = -0.364994091915365
step = 2   x = 4.15652661816414   f(x) = 0.145393647790519
step = 3   x = 3.86816299760975   f(x) = 0.0232325785022762
step = 4   x = 3.80257728615178   f(x) = 0.000846462445067031
step = 5   x = 3.80000367572973   f(x) = 1.20550697590982e-6
step = 6   x = 3.80000000000748   f(x) = 2.45159448297727e-12
3.80000000000748
7.81024967590665

show (pl1 + pf1 + ord, aspect_ratio = 1/1, figsize = 9)

bool (LL (xmin - 1e-8) > fmin); bool (LL (xmin - 1e-7) > fmin)

False
True

False
True

bool (LL (xmin + 1e-8) > fmin); bool (LL (xmin + 1e-7) > fmin); bool (LL (xmin + 1e-6) > fmin)

False
False
True

False
False
True

plot (LL, xmin - 5e-7, xmin + 5e-7)

xmin, st = min_nr (LL, 5., tolf = 1.e-13, n_steps = True)
xmin, st

(3.80000000000000, 7)

(3.80000000000000, 7)

fmin = LL (xmin)
bool (LL (xmin - 1e-8) > fmin); bool (LL (xmin + 1e-8) > fmin)

False
True

False
True

L

x |--> sqrt((x - x_d)^2 + y_d^2) + sqrt((x - x_v)^2 + y_v^2)

x |--> sqrt((x - x_d)^2 + y_d^2) + sqrt((x - x_v)^2 + y_v^2)

min_nr (L.subs (x_v = xyv[0], y_v = xyv[1], x_d = xyd[0], y_d = xyd[1]), 5., tolf = 1.e-12)

3.80000000000000

3.80000000000000

(*) Crteži Dona Quijotea, Sancha Panze i vjetrenjača posuđeni su s omotnice albuma Windmill Tilter Kena Wheelera i Orkestra Johna Dankwortha iz 1969. godine.

PPPK_01

349 days ago by fresl