Mehanika_1-06_Prostorni_sistemi_(v0.5)

Funkcije koje smo definirali u prethodnim radnim listovima uvedene su u i ovaj radni list.  

Mehanika 1.

Prostorni spojeni sistemi

Poopćeni pomaci tijela u prostoru

[Natuknice možete naći i u datoteci  Prostorni spojeni sistemi  u  Bilješkama i skicama s predavanja iz Mehanike 1.]

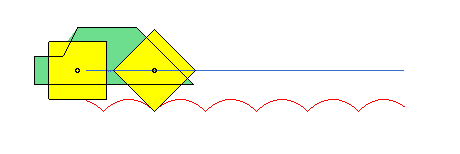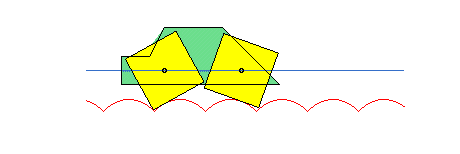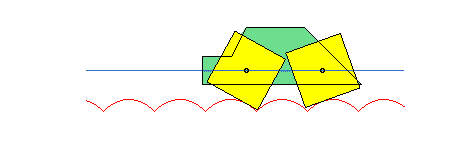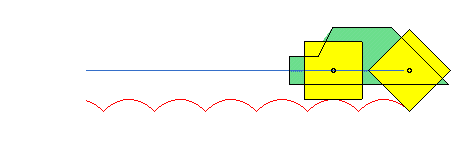
Pomak krutoga tijela možemo prikazati kao kompoziciju pomaka po pravcu (translacije) odabrane točke tijela i zaokreta (rotacije) tijela oko osi koja prolazi tom točkom.

U primjeru ćemo uzeti da je tijelo kvadar. U početnom je položaju jedan njegov vrh u ishodištu koordinatnoga sustava, a tri brida leže na koordinatnim osima.

Pomak po pravcu (translacijski pomak)

Pri translacijskom se pomaku tijela sve njegove točke pomiču za isti vektor, pa je translacijski pomak tijela određen translacijskim pomakom neke, bilo koje njegove točke.

Translacijskim pomakom za vektor $\vec{p}$ točka $A$, čiji je početni položaj određen radijus–vektorom  $\vec{a} = \vec{r}_{\!A}$,  dolazi u novi položaj

$\vec{a}_{\mathrm{transl}} \,=\, \vec{a} + \vec{p}$.

Točku i točke u listi translatiramo funkcijama 

translate_point (a, t)

• a — radijus–vektor točke
• t — vektor pomaka

translate_point_list (la, t)

• la — lista radijus–vektora točaka

Vektor pomaka možemo zadati pomoću pravca po kojem se promatrana točka kreće i duljine pomaka. Budući da su po pravcu moguća dva smisla gibanja, odabrat ćemo na njemu orijentaciju i uvesti pojam orijentirane duljine koja, za razliku od „klasične” duljine, može biti pozitivna ili negativna, ovisno o smislu gibanja po orijentiranome pravcu. Orijentirani pravac u prostoru (točnije, skup svih međusobno usporednih pravaca) određen je s dva kuta (na prvome predavanju označili smo ih sa $\varphi$ i $\psi$). Budući da je orijetirana duljina pomaka (po zadanom pravcu) određena jednim brojem, translacijski je pomak određen s tri broja.

Vektor u prostoru možemo rastaviti u tri komponente; ako te komponente nisu usporedne s jednom ravninom, rastav je jedinstven. I obrnuto, tri komponente koje nisu usporedne s jednom ravninom određuju jedan i samo jedan vektor. Najčešće je pogodno vektor pomaka rastaviti u komponente usporedne s koordinatnim osima ili zadati pomak trima komponentama usporednima s koordinatnim osima:

$\vec{p} \:=\: \vec{u} \,+\, \vec{v} \,+\, \vec{w} \:=\: u\,\vec{\imath} \,+\, v\,\vec{\jmath} \,+\, w\,\vec{k}$; 

skalarne komponente $u,\,v$ i $w$ tri su broja kojima je zadan pomak. Translacijski se pomak, dakle, može zadati na više načina, ali uvijek su potrebna tri broja — kažemo da tijelo i točka u prostoru imaju tri translacijska stupnja slobode.

• vektor pomaka:

• pomak tijela:

... uočite da su svi bridovi kvadra u krajnjem položaju usporedni s odgovorajućim bridovima u početnom položaju. 

• rastavljanje vektora pomaka u komponente usporedne s koordinatnim osima:

Zaokret (rotacijski pomak)

Tijelo koje rotira oko točke u svakom trenutku rotira oko nekog pravca koji nazivamo trenutnom osi rotacije, a ta os može mijenjati svoj položaj, prolazeći uvijek središtem rotacije. Ograničit ćemo se stoga na rotaciju točke i tijela oko osi.

Rotacijom oko osi $o$, koja prolazi ishodištem, za kut $\rho$ točka $A$, početni položaj koje je određen radijus–vektorom $a$, dolazi u točku

$\vec{a}_{\mathrm{rot}} \,=\, \mathcal{R}\,\vec{a}$,

gdje je $\mathcal{R}$ operator rotacije.  U odabranom se koordinatnom sustavu operator rotacije $\mathcal{R}$ prikazuje matricom $\mathbf{R}$, pa možemo pisati i

$\vec{a}_{\mathrm{rot}} \,=\, \mathbf{R}\,\vec{a}$,

pri čemu prešutno uzimamo da su vektori $\vec{a}$ i $\vec{a}_{\mathrm{rot}}$ rastavljeni u komponente u tom istom koordinatnom sustavu.

Točku i točke u listi rotiramo funkcijama 

rotate_point (o, rho, a)

• a — radijus–vektor točke
• o — vektor kojim je određena os rotacije
  
• rho — kut rotacije
  

rotate_point_list (o, rho, la)

• la — lista radijus–vektora točaka

Nastavak primjera:

• zaokret tijela oko osi $z$:

• zaokret tijela oko osi $y$:

• slijed zaokretâ tijela oko osî $z$ i $y$:

... oko osi $z$ ...

... pa oko osi $y$ ...

... konačan položaj

• slijed zaokretâ tijela oko osî $y$ i $z$:

... oko osi $y$ ...

... pa oko osi $z$ ...

... konačan položaj

• rotacija nije komutativna operacija — različiti sljedovi zaokreta (oko istih osi) završavaju tijelom u različitim položajima:

• zaokret tijela oko osi određene vektorom  $\vec{o} = \vec{\jmath} + \vec{k}$:

• rotacije oko koordinatnih osî nisu komponente rotacije oko opće osi:

Zaokret u teoriji „malih” pomaka

U teoriji „malih” pomaka putovanje točke po kružnici zamjenjujemo putovanjem po tangenti na kružnicu u točki koja određuje početni položaj. Novi položaj točke $A$ određuje se prema izrazu

$\vec{a}_{\mathrm{rmp}} \:=\: \vec{a} \,+\, \vec{\varrho}\times\vec{a}$,

gdje je $\vec{a}$ radijus–vektor kojim je određen početni položaj točke $A$, dok je $\vec{\varrho}$ vektor zaokreta: ako su $\varrho_x,\, \varrho_y$ i $\varrho_z$ kutovi zaokreta oko osî $x,\, y,\, z$, onda je

$\vec{\varrho} \,=\, \varrho_x\,\vec{\imath} + \varrho_y\,\vec{\jmath} + \varrho_z\,\vec{k}$.

Vektor $\vec{\varrho}$ leži na osi rotacije; i sada uzimamo da os rotacije prolazi ishodištem.

Vektor  $\vec{\varrho}\times\vec{a}$  vektor je pomaka točke $A$. Okomit je na vektor $\vec{\varrho}$. Stavimo li početak vektora  $\vec{\varrho}\times\vec{a}$  u točku $A$, ležat će u ravnini koja prolazi točkom $A$, a okomita je na vektor $\vec{\varrho}$, a time i na os rotacije. U toj je ravnini, prema tome, kružnica po kojoj točka $A$ stvarno putuje. Kako je vektor  $\vec{\varrho}\times\vec{a}$  okomit i na vektor $\vec{a}$, okomit je na ravninu koju ta dva vektora razapinju. Na presječnici te ravnine i ravnine spomenute kružnice radijus je kružnice. Slijedi da je vektor  $\vec{\varrho}\times\vec{a}$  okomit na radijus kružnice, a kako leži u njezinoj ravnini, na njezinoj je tangenti.

Nastavak primjera:

• „zaokret” tijela oko osi $z$:

... usporedba s „pravim” zaokretom:

• „zaokret” tijela oko osi $y$:

... usporedba s „pravim” zaokretom:

• slijed „zaokreta” tijela oko osî $z$ i $y$:

... oko osi $z$ ...

... pa oko osi $y$ ...

... konačan položaj

... usporedba s nizom „pravih” zaokreta:

• slijed „zaokreta” tijela oko osî $y$ i $z$:

... oko osi $y$ ...

... pa oko osi $z$ ...

... konačan položaj

• i u teoriji „malih” pomaka različiti sljedovi „zaokreta” (oko istih osi) završavaju s tijelom u različitim položajima:

• „zaokret” tijela oko osi određene vektorom  $\vec{o} \,=\, \vec{\jmath} + \vec{k}$:

... usporedba s „pravim” zaokretom:

... usporedbe s nizovima „zaokreta” oko osî:

Ni u teoriji „malih” pomaka, prema tome, „rotacije” oko koordinatnih osî nisu komponente „rotacije” oko opće osi. 

Ali, ako su kutovi dovoljno mali, za kompoziciju „rotacija” vrijedi

$\mathcal{L}_2\, (\mathcal{L}_1\, \vec{a}) \;=\; \mathcal{L}_2\, (\vec{a} \,+\, \vec{\varrho}_1\times\vec{a})$

$\phantom{\mathcal{L}_2\, (\mathcal{L}_1\, \vec{a})} \;=\; (\vec{a} \,+\, \vec{\varrho}_1\times\vec{a}) \:+\: \vec{\varrho}_2\times (\vec{a} \,+\, \vec{\varrho}_1\times\vec{a})$

$\phantom{\mathcal{L}_2\, (\mathcal{L}_1\, \vec{a})} \;=\; \vec{a} \:+\: \vec{\varrho}_1\times\vec{a} \:+\: \vec{\varrho}_2\times\vec{a} \:+\: \vec{\varrho}_2\times(\vec{\varrho}_1\times\vec{a})$

$\phantom{\mathcal{L}_2\, (\mathcal{L}_1\, \vec{a})} \;=\; \vec{a} \:+\: (\vec{\varrho}_1\,+\, \vec{\varrho}_2)\times\vec{a} \:+\: \varrho_2\,\vec{e}_2\times(\varrho_1\,\vec{e}_1\times\vec{a})$

$\phantom{\mathcal{L}_2\, (\mathcal{L}_1\, \vec{a})} \;=\; \vec{a} \:+\: (\vec{\varrho}_1\,+\, \vec{\varrho}_2)\times\vec{a} \:+\: \underbrace{\varrho_1\,\varrho_2}_{\textstyle\approxeq 0}\,[\vec{e}_2\times(\vec{e}_1\times\vec{a})]$

$\phantom{\mathcal{L}_2\, (\mathcal{L}_1\, \vec{a})} \;\approxeq\; \vec{a} \:+\: (\vec{\varrho}_1\,+\, \vec{\varrho}_2)\times\vec{a}$

$\phantom{\mathcal{L}_2\, (\mathcal{L}_1\, \vec{a})} \;=\; \vec{a} \:+\: (\vec{\varrho}_2\,+\, \vec{\varrho}_1)\times\vec{a}$

$\phantom{\mathcal{L}_2\, (\mathcal{L}_1\, \vec{a})}\;=\; \mathcal{L}_1\,(\mathcal{L}_2\,\vec{a}).$

Prema tome, za dovoljno male kutove „rotacija” jest komutativna operacija, a kompozicija se „rotacija” može prikazati pomoću zbrajanja.