DKiPI_3_2019_studenti

Zadavanje vektora i matrica, osnovne naredbe i operacije

- MPZI_predavanje_02 i MPZI_vj02 - vektori i matrice

Vektor se zadaje nizom brojeva (listom brojeva)

Broj komponenata vektora (nazvan i njegovom dimenzijom ili dimenzijom vektorskog prostora kojem pripada) daju funkcije

Pristupanje komponentama vektora vrši se indeksiranjem (prvi element liste ima indeks 0!)

Za vektore sa $n$ komponenata ($n$-dimenzionalne vektore) skalarni je umnožak  $s = \mathbf{a}\cdot\mathbf{b} = \displaystyle\sum_{i=0}^{n-1}\, a_i\, b_i$.

Skalarni produkt vektora u matričnoj notaciji:

                                                                             $\mathbf{a}\cdot\mathbf{b} = \mathbf{a}^T \mathbf{b}$

Matrice

Osnovni način zadavanja matrica je nizom čije su komponenete nizovi brojeva jednakih duljina

Pristupanje komponentama matrice:

Pristupanje cijelom retku ili cijelom stupcu matrice:

Pristupanje 'podmatricama':

Konstruiranje jedinične matrice B reda 4x4

Vektor možemo "pretvoriti" u jednorednu ili u jednostupčanu matricu:

Umnožak $\mathbf{C} = \mathbf{A\,B}$ dviju matrica $\mathbf{A}$ i $\mathbf{B}$ definiran je ako je broj stupaca prve jednak broju redaka druge, jer je opći izraz za komponente umnoška  $c_{i,j} = \displaystyle\sum_{k = 0}^{n - 1} a_{i,k}\,b_{k,j}$, gdje je $n$ broj stupaca prve i broj redaka druge matrice.

Produkt vektora  $\mathbf{a} \mathbf{b}^T$  daje matricu.

Da bi primjenili operacije s matricama na vektore, prvo ih je potrebno transformirati u jednoredne ili jednostupčane matrice

Vektor se, u stvari, u određenim kontekstima može smatrati jednostupčanom matricom i bez eksplicitne prevorbe, tako da je definirano i množenje matrice i vektora; rezultat je vektor (a ne jednostupčana matrica):

Transponirana matrica: $\mathbf{A}^T$

Inverzna matrica: $\mathbf{A}^{-1}$

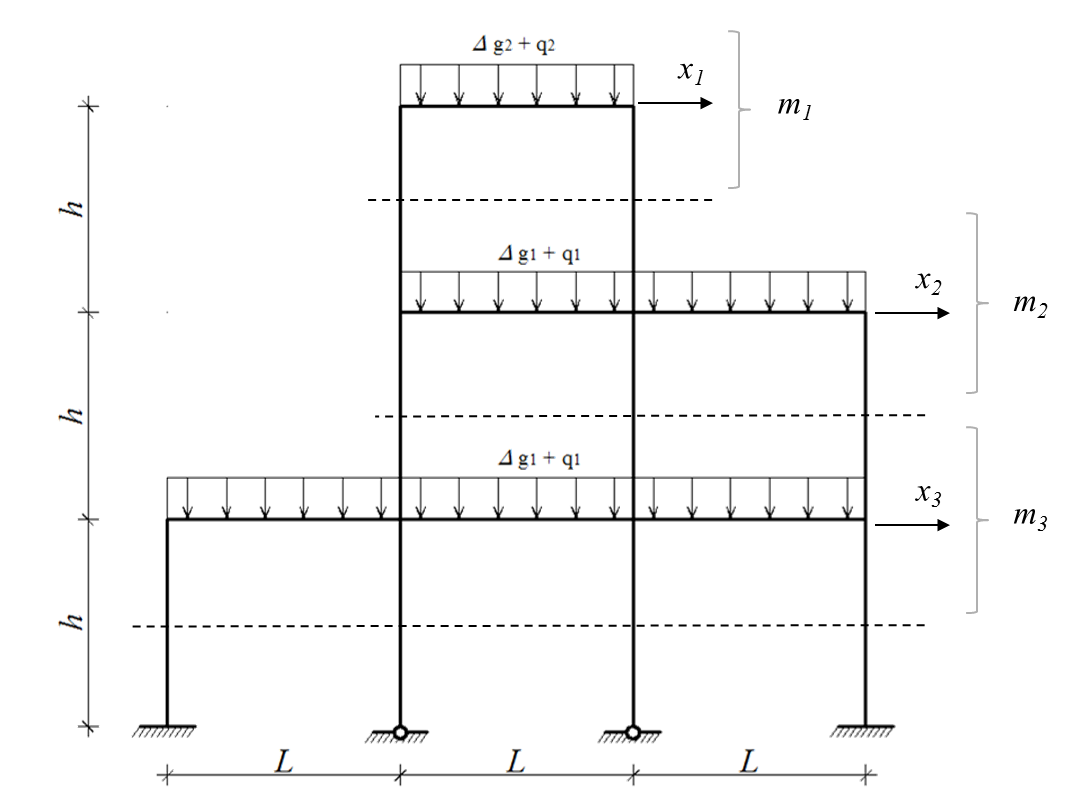
DKPI - ZADATAK

Za zadani okvir potrebno je odabrati dinamičke stupnjeve slobode te za odabrani model odrediti oblike titranja metodom Stodola.

Zatim treba odrediti zakon prisilnog titranja sustava koje će nastati od naglog ubrzanja podloge $u_g(t) = 0,25 g$ trajanja 4 s.

Matrica krutosti

Kondenzacija matrice krutosti:

                                                  $\mathbf{K} = \mathbf{k}_{tt} - \mathbf{k}_{t0} \mathbf{k}_{00}^{-1} \mathbf{k}_{0t}$

Matrica fleksibilnosti:

                                  $\mathbf{F} = \mathbf{k}^{-1}$

Matrica masa

Matrica masa

Odredivanje vlastitih frekvencija i vektora metodom Stodola

$\mathbf{D} v_m^{(n)} = \lambda_m v_m^{(n+1)}$

gdje je : $\mathbf{D} = \mathbf{F} \;\mathbf{M}$      i      $\lambda_m = \frac{1}{\omega_m^2}$

Da bi proveli iterativni postupak metode Stodola, programirati će se jednostavna funkcija koja izvršava iterativni proces do zadovoljenja zadanog uvjeta konvergencije

Više o osnovama programiranja: 

- MPZI_predavanje_09 i MPZI_vj09

- MPZI_predavanje_10 i MPZI_vj10

- MPZI_predavanje_11 i MPZI_vj11

- MPZI_predavanje_12 i MPZI_vj12

- MPZI_predavanje_13 i MPZI_vj13

"Programska se funkcija definira na sljedeći način:

    def naziv (parametri) :

        tijelo funkcije

Definicija funkcije započinje ključnom riječju def iza koje slijedi naziv funkcije. Dobro odabrani naziv trebao bi biti ključem značenja i svrhe funkcije. Nakon naziva se između okruglih zagrada navode parametri funkcije. Parametri su varijable koje pri upotrebi funkcije prihvaćaju vrijednosti koje se prenose u funkciju—koje ulaze u nju. (Par zagrada treba napisati i ako funkcija nema parametara.) Prvi redak definicije funkcije završava dvotočkom.

Tijelo funkcije niz je naredbi koje propisuju kako funkcija radi ono čemu je namijenjena.

Vrijednost koju funkcija izračunava i 'vraća' naredbom return je vrijednost funkcije.

Upotreba funkcije naziva se pozivom funkcije: 

       naziv (argumenti)

Nakon naziva se između okruglih zagrada navode funkcijski argumenti—vrijednosti koje se prenose u funkciju."

.

Iteracija:   

$\mathbf{D} v_m^{(n)} = \lambda_m v_m^{(n+1)}$

uvjet konvergencije $\Delta = \vert \lambda_m^{(n+1)} - \lambda_m^{(n)} \vert < 10^{-6}$

1. oblik

2. oblik

Matrica čišćenja:

$\mathbf{S}_1 = \mathbf{I} - \frac{\mathbf{\phi}_1 \mathbf{\phi}_1^T \mathbf{M}}{\mathbf{\phi}_1^T \mathbf{M} \mathbf{\phi}_1}$

Nova dinamička matrica ('očišćena od prvog oblika'):

$\mathbf{D}_1 = \mathbf{D} \mathbf{S}_1$

Normiranje vektora $\mathbf{v}_2$ na jedinicu

2. oblik

Matrica čišćenja:

$\mathbf{S}_2 = \mathbf{S}_1 - \frac{\mathbf{\phi}_2 \mathbf{\phi}_2^T \mathbf{M}}{\mathbf{\phi}_2^T \mathbf{M} \mathbf{\phi}_2}$

Normiranje vektora $\mathbf{v}_3$ na jedinicu

Normiranje vektora $\mathbf{\phi}_2$ na jedinicu

Periodi:

Modalna analiza

$\mathbf{u} = \mathbf{\Phi} \mathbf{q}$

$M_n\ddot{q}_n + K_n q_n = P_n(t)$     n=1,2,3

gdje je: $M_n = \mathbf{\phi}_n^T \mathbf{m} \mathbf{\phi}_n$; $K_n = \mathbf{\phi}_n^T \mathbf{k}\mathbf{\phi}_n$ i $P_n = \mathbf{\phi}_n^T \mathbf{p}_{eff}$

Efektivno opterećenje za horizontalno gibanje podloge:

$\mathbf{p}_{eff}(t) = - \mathbf{M}\mathbf{l} u_g(t)$

gdje je $\mathbf{l}$ vektor utjecaja