DKiPI_1_2019_s izradom -- Sage

Uvodno o programskom sustavu za simboličku matematiku Sage (http://sagemath.org/) - MPZI_predavanje_01

Zadaci za 'zagrijavanje' - MPZI_vj01 - aritmetičke operacije i matematičke funkcije

- MPZI_predavanje_02 i MPZI_vj02 - izrazi, funkcije, polinomi i njihovi grafovi

- MPZI_predavanje_03 i MPZI_vj03 - grafika - prikaz ravninskih i prostornih krivulja

- MPZI_predavanje_04 i MPZI_vj04 - prikaz ploha i nivo krivulja

- MPZI_predavanje_05 i MPZI_vj05 - vektori i matrice

- MPZI_predavanje_06 i MPZI_vj06 - jednadžbe i nejednadžbe (bitno $\rightarrow$ sustavi linearnih jednadžbi i određivanje korijena polinoma)

- MPZI_predavanje_07 i MPZI_vj07 - Elementi matematičke analize (derivacije!)

- MPZI_predavanje_08 i MPZI_vj08 - Elementi matematičke analize (2) (Integrali, uvod u diferencijalne jednadžbe)

DKPI - slobodno titranje sustava s jednim stupnjem slobode

Matematički model slobodnog neprigušenog titranja:

$m \ddot{u}(t) + k u(t) = 0$

$\ddot{u}(t) + \omega_n^2 u(t) = 0$

gdje je $\omega^2_n = \frac{k}{m}$ prirodna kružna frekvencija sustava

Zadavanje varijabli i nepoznatih funkcija:

var('omega_n, t')
u = function('u')(t)

Zadavanje diferencijalne jednadžbe (izraza):

de1 = diff(u, t, 2) + omega_n^2*u == 0
de1

$\newcommand{\Bold}[1]{\mathbf{#1}}\omega_{n}^{2} u\left(t\right) + \frac{\partial^{2}}{(\partial t)^{2}}u\left(t\right) = 0$

Određivanje rješenja diferencijalne jednadžbe

desolve( de1, u, ivar=t)

Traceback (click to the left of this block for traceback)
...
Is omega_n zero or nonzero?

Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
  File "_sage_input_13.py", line 10, in <module>
    exec compile(u'open("___code___.py","w").write("# -*- coding: utf-8 -*-\\n" + _support_.preparse_worksheet_cell(base64.b64decode("ZGVzb2x2ZSggZGUxLCB1LCBpdmFyPXQp"),globals())+"\\n"); execfile(os.path.abspath("___code___.py"))
  File "", line 1, in <module>
    
  File "/tmp/tmpyCIwJV/___code___.py", line 2, in <module>
    exec compile(u'desolve( de1, u, ivar=t)
  File "", line 1, in <module>
    
  File "/opt/SageMath/local/lib/python2.7/site-packages/sage/calculus/desolvers.py", line 584, in desolve
    soln = P(cmd)
  File "/opt/SageMath/local/lib/python2.7/site-packages/sage/interfaces/interface.py", line 280, in __call__
    return cls(self, x, name=name)
  File "/opt/SageMath/local/lib/python2.7/site-packages/sage/interfaces/interface.py", line 695, in __init__
    raise TypeError(x)
TypeError: Computation failed since Maxima requested additional constraints; using the 'assume' command before evaluation *may* help (example of legal syntax is 'assume(omega_n>0)', see `assume?` for more details)
Is omega_n zero or nonzero?

zadajemo pretpostavku da je $\omega_n \neq 0$

assume(omega_n != 0)

Rješenje diferencijalne jednadžbe glasi:

desolve( de1, u, ivar=t)

$\newcommand{\Bold}[1]{\mathbf{#1}}K_{2} \cos\left(\omega_{n} t\right) + K_{1} \sin\left(\omega_{n} t\right)$

$K_1$ i $K_2$ su nepoznate konstante integracije diferencijalne jednadžbe i ovise o početnim uvjetima.

Određivanje rješenja diferencijalne jednadžbe za zadane početne uvjete $u_0$ i $v_0$

NAPOMENA:

početni uvjeti upisuju se u obliku liste:

[ $t_0$ , $u(t_0) = u_0$ ] za problem početne vrijednosti u diferencijalnoj jednadžbi 1. reda

[ $t_0$ , $u(t_0) = u_0$ , $u'(t_0)=v_0$ ] za problem početne vrijednosti u diferencijalnoj jednadžbi 2. reda

[ $x_0$ , $y(x_0)$ , $x_1$ , $y(x_1)$ ] za problem rubnih vrijednosti u diferencijalnoj jednadžbi 2. reda

var('u0, v0')   #za rješenje u opcem obliku uvodimo nove simboličke konstante za početne uvjete

$\newcommand{\Bold}[1]{\mathbf{#1}}\left(u_{0}, v_{0}\right)$

rj_1 = desolve( de1, u, ivar=t, ics=[0, u0, v0])
rj_1

$\newcommand{\Bold}[1]{\mathbf{#1}}u_{0} \cos\left(\omega_{n} t\right) + \frac{v_{0} \sin\left(\omega_{n} t\right)}{\omega_{n}}$

Nacrtati vremensku funkciju odziva sustava za sljedeće parametre:

$\omega_n = 10$ , $u_0 = 0.5$ , $v_0=8$

rj_1.subs(omega_n=10, u0=0.5, v0=8)

$\newcommand{\Bold}[1]{\mathbf{#1}}0.500000000000000 \, \cos\left(10 \, t\right) + \frac{4}{5} \, \sin\left(10 \, t\right)$

rj_1.subs(omega_n=10, u0=1/2, v0=8)

$\newcommand{\Bold}[1]{\mathbf{#1}}\frac{1}{2} \, \cos\left(10 \, t\right) + \frac{4}{5} \, \sin\left(10 \, t\right)$

rj_1a = rj_1.subs(omega_n=10, u0=1/2, v0=8)
rj_1a

$\newcommand{\Bold}[1]{\mathbf{#1}}\frac{1}{2} \, \cos\left(10 \, t\right) + \frac{4}{5} \, \sin\left(10 \, t\right)$

rj_1

$\newcommand{\Bold}[1]{\mathbf{#1}}u_{0} \cos\left(\omega_{n} t\right) + \frac{v_{0} \sin\left(\omega_{n} t\right)}{\omega_{n}}$

s1 = plot( rj_1a, [0, 5], color = "red")
s1

Matematički model slobodnog prigušenog titranja:

$m \ddot{u}(t) +c \dot{u}(t)+ k u(t) = 0$

$\ddot{u}(t) +2\omega_n \zeta \dot{u}(t)+ \omega_n^2 x(t) = 0$

gdje je $\zeta = \frac{c}{c_{kr}}$ relativno prigušenje sustava - omjer ekvivalentnog viskoznog prigušenja ( $c$ ) i kritičnog prigušenja sustava ( $c_{kr} = 2 \omega_n m$ )

var('m, c, k, zeta, omega_d')

$\newcommand{\Bold}[1]{\mathbf{#1}}\left(m, c, k, \zeta, \omega_{d}\right)$

de2 = m*diff(u, t, 2) + c*diff(u, t) + k*u == 0
de2

$\newcommand{\Bold}[1]{\mathbf{#1}}k u\left(t\right) + c \frac{\partial}{\partial t}u\left(t\right) + m \frac{\partial^{2}}{(\partial t)^{2}}u\left(t\right) = 0$

desolve( de2, u, ivar=t)

Traceback (click to the left of this block for traceback)
...
Is 4*k*m-c^2 positive, negative or zero?

Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
  File "_sage_input_28.py", line 10, in <module>
    exec compile(u'open("___code___.py","w").write("# -*- coding: utf-8 -*-\\n" + _support_.preparse_worksheet_cell(base64.b64decode("ZGVzb2x2ZSggZGUyLCB1LCBpdmFyPXQp"),globals())+"\\n"); execfile(os.path.abspath("___code___.py"))
  File "", line 1, in <module>
    
  File "/tmp/tmp8etU5f/___code___.py", line 2, in <module>
    exec compile(u'desolve( de2, u, ivar=t)
  File "", line 1, in <module>
    
  File "/opt/SageMath/local/lib/python2.7/site-packages/sage/calculus/desolvers.py", line 584, in desolve
    soln = P(cmd)
  File "/opt/SageMath/local/lib/python2.7/site-packages/sage/interfaces/interface.py", line 280, in __call__
    return cls(self, x, name=name)
  File "/opt/SageMath/local/lib/python2.7/site-packages/sage/interfaces/interface.py", line 695, in __init__
    raise TypeError(x)
TypeError: Computation failed since Maxima requested additional constraints; using the 'assume' command before evaluation *may* help (example of legal syntax is 'assume(4*k*m-c^2>0)', see `assume?` for more details)
Is 4*k*m-c^2 positive, negative or zero?

Sjetimo se da je ovo upravo diskriminanta karakteristične jednadžbe, te da karakter titranja ovisi o njenoj vrijednosti

Kritično prigušenje - diskriminanta izčezava

assume( 4*k*m - c^2 == 0)

desolve( de2, u, ivar=t)

Traceback (click to the left of this block for traceback)
...
Is c zero or nonzero?

Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
  File "_sage_input_30.py", line 10, in <module>
    exec compile(u'open("___code___.py","w").write("# -*- coding: utf-8 -*-\\n" + _support_.preparse_worksheet_cell(base64.b64decode("ZGVzb2x2ZSggZGUyLCB1LCBpdmFyPXQp"),globals())+"\\n"); execfile(os.path.abspath("___code___.py"))
  File "", line 1, in <module>
    
  File "/tmp/tmpQpkxnl/___code___.py", line 2, in <module>
    exec compile(u'desolve( de2, u, ivar=t)
  File "", line 1, in <module>
    
  File "/opt/SageMath/local/lib/python2.7/site-packages/sage/calculus/desolvers.py", line 584, in desolve
    soln = P(cmd)
  File "/opt/SageMath/local/lib/python2.7/site-packages/sage/interfaces/interface.py", line 280, in __call__
    return cls(self, x, name=name)
  File "/opt/SageMath/local/lib/python2.7/site-packages/sage/interfaces/interface.py", line 695, in __init__
    raise TypeError(x)
TypeError: Computation failed since Maxima requested additional constraints; using the 'assume' command before evaluation *may* help (example of legal syntax is 'assume(c>0)', see `assume?` for more details)
Is c zero or nonzero?

assume(c != 0)

rj_2 = desolve( de2, u, ivar=t, ics=[0, u0, v0])
rj_2

$\newcommand{\Bold}[1]{\mathbf{#1}}\frac{1}{2} \, {\left(\frac{{\left(c u_{0} + 2 \, m v_{0}\right)} t}{m} + 2 \, u_{0}\right)} e^{\left(-\frac{c t}{2 \, m}\right)}$

Ako supstituiramo izraz za krtično prigušenje $c_{kr} = 2 m \omega_n$

rj_2a = rj_2.subs(c = 2*m*omega_n).simplify_full()
rj_2a

$\newcommand{\Bold}[1]{\mathbf{#1}}{\left({\left(\omega_{n} t + 1\right)} u_{0} + t v_{0}\right)} e^{\left(-\omega_{n} t\right)}$

rj_2b = rj_2a.subs(omega_n=10, u0=1/2, v0=8)
rj_2b

$\newcommand{\Bold}[1]{\mathbf{#1}}\frac{1}{2} \, {\left(26 \, t + 1\right)} e^{\left(-10 \, t\right)}$

s2 = plot(rj_2b, [t, 0, 5], color="blue")
s2

b) Prigušenje manje od kritičnog

forget( 4*k*m - c^2 == 0)
assume( 4*k*m - c^2 > 0 )

desolve( de2, u, ivar=t)

$\newcommand{\Bold}[1]{\mathbf{#1}}{\left(K_{2} \cos\left(\frac{1}{2} \, t \sqrt{-\frac{c^{2}}{m^{2}} + \frac{4 \, k}{m}}\right) + K_{1} \sin\left(\frac{1}{2} \, t \sqrt{-\frac{c^{2}}{m^{2}} + \frac{4 \, k}{m}}\right)\right)} e^{\left(-\frac{c t}{2 \, m}\right)}$

rj_3 = desolve( de2, u, ivar=t, ics=[0, u0, v0])
rj_3

$\newcommand{\Bold}[1]{\mathbf{#1}}{\left(u_{0} \cos\left(\frac{1}{2} \, t \sqrt{-\frac{c^{2}}{m^{2}} + \frac{4 \, k}{m}}\right) + \frac{{\left(c u_{0} + 2 \, m v_{0}\right)} \sin\left(\frac{1}{2} \, t \sqrt{-\frac{c^{2}}{m^{2}} + \frac{4 \, k}{m}}\right)}{m \sqrt{-\frac{c^{2}}{m^{2}} + \frac{4 \, k}{m}}}\right)} e^{\left(-\frac{c t}{2 \, m}\right)}$

rj_3a = rj_3.subs(c = zeta*2*m*omega_n, k = m*omega_d^2 + m*omega_n^2*zeta^2).simplify_full()
rj_3a.show()

$\newcommand{\Bold}[1]{\mathbf{#1}}\frac{{\left(\omega_{n} u_{0} \zeta \sin\left(\sqrt{\omega_{d}^{2}} t\right) + \sqrt{\omega_{d}^{2}} u_{0} \cos\left(\sqrt{\omega_{d}^{2}} t\right) + v_{0} \sin\left(\sqrt{\omega_{d}^{2}} t\right)\right)} e^{\left(-\omega_{n} t \zeta\right)}}{\sqrt{\omega_{d}^{2}}}$

gdje je $\omega_d = \omega \sqrt{1 - \zeta^2}$ frekvencija prigušenog titranja

Sjetimo se da za $\zeta << 1$ , slijedi da je $\omega_d \approx \omega$

Neka je relativno prigušenje zadanog sustava $3\%$

s3 = plot(rj_3a(omega_d = omega_n*sqrt(1-zeta^2))(omega_n=10, u0=1/2, v0=8, zeta=0.03), [0, 5], color="green")
s3

c) Prigušenje veće od kritičnog

forget( 4*k*m - c^2 > 0)
assume( 4*k*m - c^2 < 0)

desolve( de2, u, ivar=t)

$\newcommand{\Bold}[1]{\mathbf{#1}}K_{2} e^{\left(-\frac{1}{2} \, t {\left(\sqrt{\frac{c^{2}}{m^{2}} - \frac{4 \, k}{m}} + \frac{c}{m}\right)}\right)} + K_{1} e^{\left(\frac{1}{2} \, t {\left(\sqrt{\frac{c^{2}}{m^{2}} - \frac{4 \, k}{m}} - \frac{c}{m}\right)}\right)}$

desolve( de2, u, ivar=t).subs(c = 2*zeta*m*omega_n, k = omega_n^2*zeta^2*m - m*omega_d^2).simplify_full().show()

$\newcommand{\Bold}[1]{\mathbf{#1}}{\left(K_{1} e^{\left(2 \, \sqrt{\omega_{d}^{2}} t\right)} + K_{2}\right)} e^{\left(-\omega_{n} t \zeta - \sqrt{\omega_{d}^{2}} t\right)}$

rj_4 = desolve( de2, u, ivar=t, ics=[0, u0, v0])
rj_4.show()

$\newcommand{\Bold}[1]{\mathbf{#1}}\frac{{\left({\left(m \sqrt{\frac{c^{2}}{m^{2}} - \frac{4 \, k}{m}} - c\right)} u_{0} - 2 \, m v_{0}\right)} e^{\left(-\frac{1}{2} \, t {\left(\sqrt{\frac{c^{2}}{m^{2}} - \frac{4 \, k}{m}} + \frac{c}{m}\right)}\right)}}{2 \, m \sqrt{\frac{c^{2}}{m^{2}} - \frac{4 \, k}{m}}} + \frac{{\left({\left(m \sqrt{\frac{c^{2}}{m^{2}} - \frac{4 \, k}{m}} + c\right)} u_{0} + 2 \, m v_{0}\right)} e^{\left(\frac{1}{2} \, t {\left(\sqrt{\frac{c^{2}}{m^{2}} - \frac{4 \, k}{m}} - \frac{c}{m}\right)}\right)}}{2 \, m \sqrt{\frac{c^{2}}{m^{2}} - \frac{4 \, k}{m}}}$

rj_4a = rj_4.subs(c = 2*zeta*m*omega_n, k = omega_n^2*zeta^2*m - m*omega_d^2).simplify_full()
rj_4a.show()

$\newcommand{\Bold}[1]{\mathbf{#1}}\frac{{\left({\left(\omega_{d}^{2} e^{\left(2 \, \sqrt{\omega_{d}^{2}} t\right)} + \omega_{d}^{2}\right)} u_{0} + {\left({\left(\omega_{n} e^{\left(2 \, \sqrt{\omega_{d}^{2}} t\right)} - \omega_{n}\right)} u_{0} \zeta + v_{0} {\left(e^{\left(2 \, \sqrt{\omega_{d}^{2}} t\right)} - 1\right)}\right)} \sqrt{\omega_{d}^{2}}\right)} e^{\left(-\omega_{n} t \zeta - \sqrt{\omega_{d}^{2}} t\right)}}{2 \, \omega_{d}^{2}}$

s4 = plot(rj_4a(omega_d = omega_n*sqrt(zeta^2-1))(omega_n=10, u0=1/2, v0=8, zeta=3), [0, 5], color="orange")
s4

show(s1 + s2 + s3 + s4)

Zadatak s auditornih vježbi:

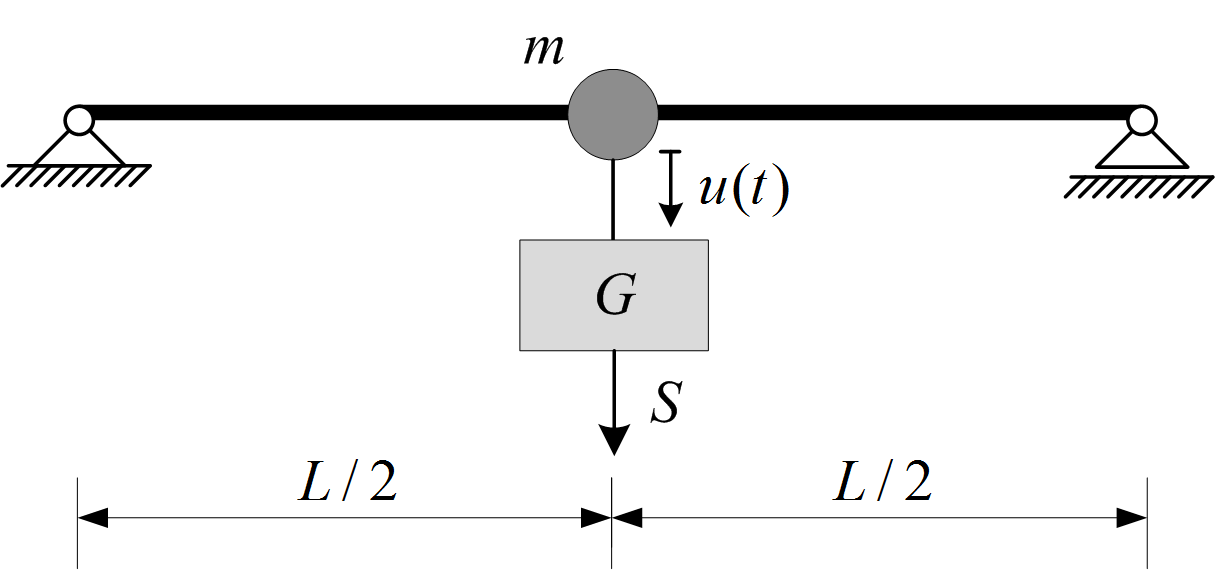
Odredi funkciju slobodnog titranja prikazane grede ako se prilikom udara impulsa sile $S=250 Ns$ naglo odvoji teret težine $G= 4kN$ . Odredi amplitudu titranja.

Zadano je: $L = 4.5 [m]$ , $m = 0,8 [t]$ , $EI = 6000 [kNm^2]$

L = 4.5
m = 0.8
EI = 6000
G = 4
S=250

k = (48*EI/L^3).n(digits=5)
omega_n = sqrt(k/m).n(digits=5)
T_n = (2*pi/omega_n).n(digits=5)
k, omega_n, T_n

$\newcommand{\Bold}[1]{\mathbf{#1}}\left(3160.5, 62.854, 0.099965\right)$

Početni pomak jednak je statičkom pomaku od tereta G

delta_st = G/k
delta_st.n(digits=3)

$\newcommand{\Bold}[1]{\mathbf{#1}}0.00127$

Početna brzina ovisi o promjeni količine gibanja koju uzrokuje impuls sile S. Budući da impuls djeluje na masu m ali i na teret težine G, u jednadžbi za promjenu količine gibanja treba uzeti ukupnu masu sustava prije titranja.

$m_{uk} \dot{u}(t_2) - m_{uk} \dot{u}(t_1) = S_{1,2}$

$\left( m + \frac{G}{g} \right) \dot{u} (0) - 0 = S$

$\dot{u} (0) = v_0 = \frac{S}{\left( m + \frac{G}{g} \right)}$

v0 = S/(m*10^3 + (G*10^3)/9.81)
v0

$\newcommand{\Bold}[1]{\mathbf{#1}}0.206996961512492$

t1 = 1

sst = plot( delta_st, [0, t1], color = 'red', ymin = -0.002, ymax = 0.002)
sst

de = m*diff(u, t, t) + k*u == 0

sol = desolve( de, u, ivar=t, ics=[t1, delta_st, v0])
sol

$\newcommand{\Bold}[1]{\mathbf{#1}}\frac{{\left(3727280092 \, \sqrt{1755829} \cos\left(\frac{3}{200} \, \sqrt{1755829} \sqrt{10}\right) - 4064051622975 \, \sqrt{10} \sin\left(\frac{3}{200} \, \sqrt{1755829} \sqrt{10}\right)\right)} \cos\left(\frac{3}{200} \, \sqrt{1755829} \sqrt{10} t\right)}{2945008173028 \, {\left(\sqrt{1755829} \cos\left(\frac{3}{200} \, \sqrt{1755829} \sqrt{10}\right)^{2} + \sqrt{1755829} \sin\left(\frac{3}{200} \, \sqrt{1755829} \sqrt{10}\right)^{2}\right)}} + \frac{{\left(4064051622975 \, \sqrt{10} \cos\left(\frac{3}{200} \, \sqrt{1755829} \sqrt{10}\right) + 3727280092 \, \sqrt{1755829} \sin\left(\frac{3}{200} \, \sqrt{1755829} \sqrt{10}\right)\right)} \sin\left(\frac{3}{200} \, \sqrt{1755829} \sqrt{10} t\right)}{2945008173028 \, {\left(\sqrt{1755829} \cos\left(\frac{3}{200} \, \sqrt{1755829} \sqrt{10}\right)^{2} + \sqrt{1755829} \sin\left(\frac{3}{200} \, \sqrt{1755829} \sqrt{10}\right)^{2}\right)}}$

sdin = plot( sol, [t1, 2], color = 'blue', plot_points=400)
sdin

show(sst + sdin, ymin = -0.004, ymax = 0.004)

DKiPI_1_2019_s izradom

2271 days ago by mdemsic@grad.hr