Prisilno titranje sustava s jednim stupnjem slobode
Na prikazani okvir djeluje dinamička sila p(t). Treba odrediti funkciju odziva sustava za različite vrijednosti funkcije sile p(t). Rješenja odrediti za homogene početne uvjete. Također odrediti i funkciju odziva za prigušenje 5% za funkcije pobude pod a) i d).
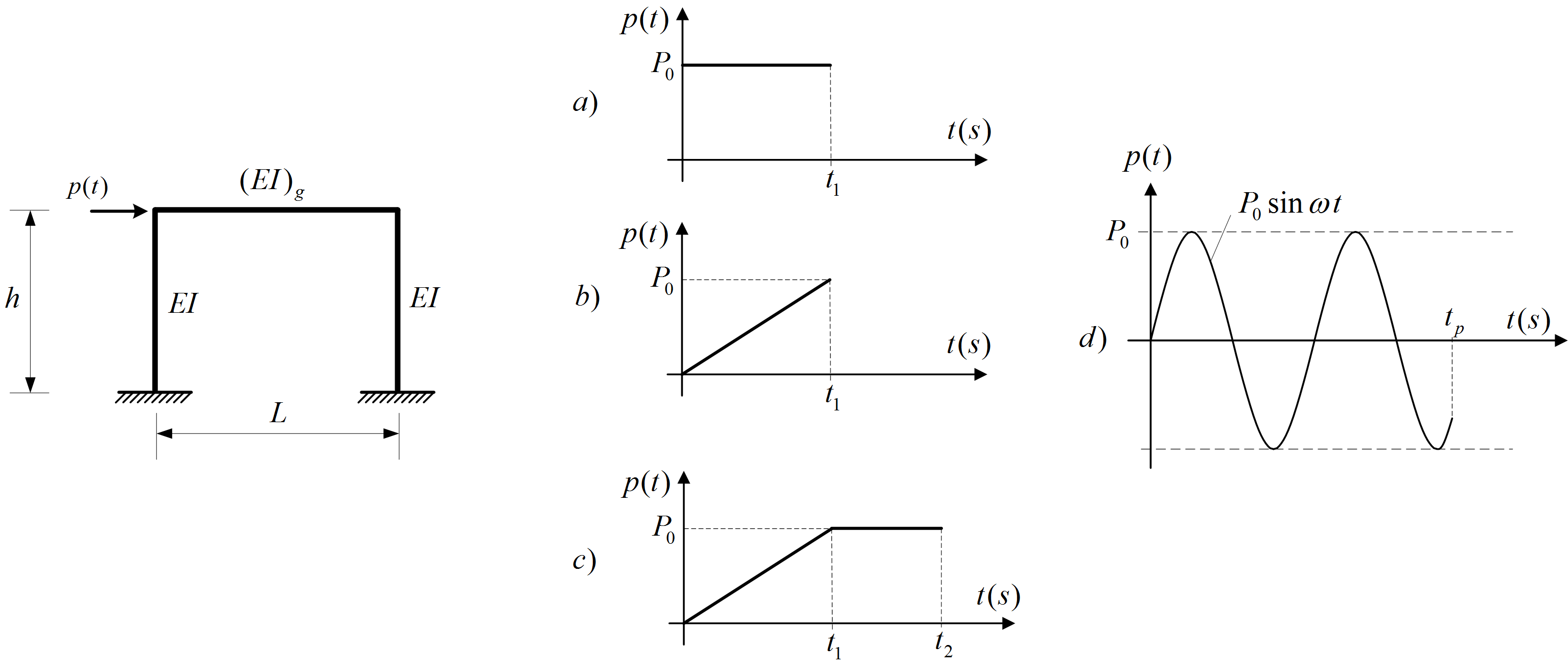
Zadano je:
$EI = 15\cdot 10^3 kNm^2$
$L = 6 m$
$h = 3 m$
$m = 3 t$
$P_0 = 20 kN$
$t_1 = 0,6 s$
$t_2 = 1 s$
Matematički model prislinog neprigušenog titranja:
$m \ddot{u}(t) + k u(t) = P(t)$
Matematički model prisilnog prigušenog titranja:
$m \ddot{u}(t) + 2 \zeta \; m \; \omega_n \dot{u} (t) + k u(t) = P(t)$
|
|
|
|
Dinamičke karakteristike sustava su:
prirodna kružna frekvencija sustava: $\omega_n = \sqrt{\frac{k}{m}}$
period slobodnog titranja: $T_n = \frac{2\pi}{\omega}$
|
|
|
|
a) Konstantna sila $P(t) = P_0$
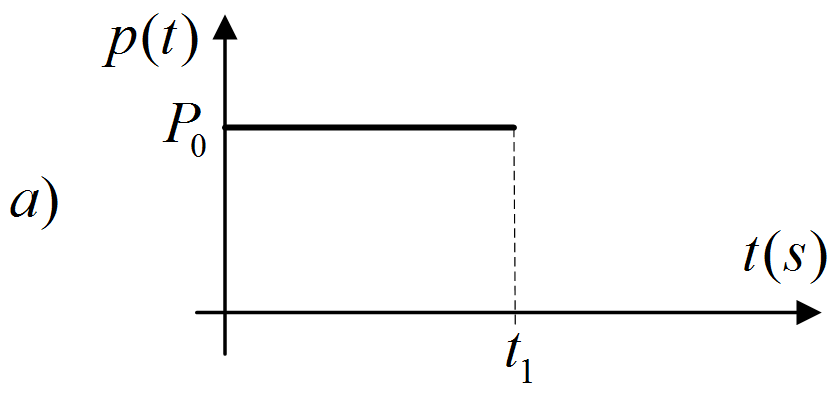
|
|
|
|
|
|
|
|
|
|
Vrijednost statičkog pomaka $u_{st} = \frac{P_0}{k}$
|
|
|
|
U trenutku $t_1 = 0.6$ s sila $P_0$ prestaje djelovati, pa za $t>0.6$ s imamo slobodno titranje
$\ddot{u}(t) + \omega_n^2 u(t) = 0$
|
|
Početne uvjete za slobodno titranje određujemo iz funkcije odziva na konstantnu silu:
$u_{t1} = u(t=0.6)$
$v_{t1} = u'(t=0.6)$
|
|
|
|
|
|
|
|
|
|
a1) Konstantna sila $P(t) = P_0$ - prigušen sustav
Matematički model prislinog prigušenog titranja:
$\ddot{u}(t) + 2 \zeta \omega_n \dot{u}(t) + \omega_n^2 u(t) = \frac{P(t)}{m}$
gdje je $\zeta$ relativno prigušenje sustava (zadano 5%).
|
|
Rješenje jednadžbe za $0 < t < t_1 $
|
|
|
|
|
|
Rješenje jednadžbe za $ t > t_1 $
|
|
|
|
|
|
|
|
b) Linearna sila P(t)
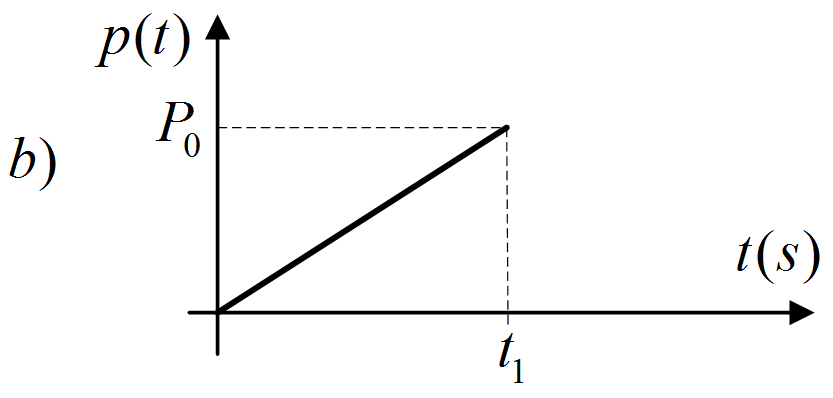
Interval $ 0 < t < t_1 $
|
|
|
|
|
|
Ako sila $P_0$ djeluje statički, pomak se također linearno povećava proporcionalno sili (nema titranja), $u_{st} = \frac{P_0}{k}\frac{t}{t_1}$
|
|
|
|
U trenutku $t_1 = 0.6$ s sila $P_0$ prestaje djelovati, pa za $t>0.6$ s imamo slobodno titranje
|
|
Početne uvjete za slobodno titranje određujemo iz prethodno određene funkcije:
$u_{t1} = u(t=0.6)$
$v_{t1} = u'(t=0.6)$
|
|
|
|
|
|
|
|
|
|
b) Linearna+konstantna sila P(t)
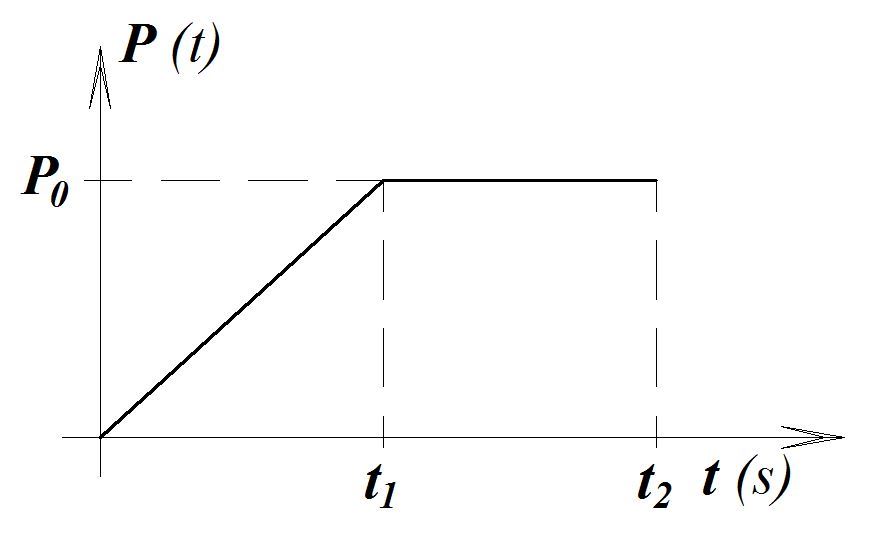
Interval $ 0 < t < t_1 $ : rješenje je ranije određeno sol_5
Interval $ t_1 < t < t_2 $
|
|
|
|
|
|
|
|
|
|
|
|
c) harmonijska pobuda $P(t) = P_0 \sin(\omega t)$
Diferencijalna jednadžba:
$m \ddot{u}(t) + k \dot{u}(t) = P_0 \sin (\omega t) $
c1) Reznancija $\omega = \omega_n$
|
|
|
|
|
|
|
|
c2) Pulsiranje (eng. bating) $\omega \approx \omega_n$
Zadajemo npr. $\omega = 0.95\omega_n$
|
|
|
|
|
|
|
|
c3) Prigušeno titranje
Diferencijalna jednadžba je:
$m \ddot{u}(t) + c \dot{u}(t) + k u(t) = P_0 \sin (\omega t) $
$\ddot{u}(t) + 2 \zeta \omega_n \dot{u}(t) + \omega_n^2 u(t) = \frac{P_0}{m} \sin (\omega t) $
Rezonancija $\omega = \omega_n$
|
|
|
|
|
|
|
|