Activate

Walks in graphs

This section provides some examples on Chapter 1 of Stanley’s book [Stanley2013].

We begin by creating a graph with 4 vertices:

sage: G = Graph(4)
sage: G
Graph on 4 vertices

This graph has no edges yet:

sage: G.vertices()
[0, 1, 2, 3]
sage: G.edges()
[]

Before we can add edges, we need to tell Sage that our graph can have loops and multiple edges.:

sage: G.allow_loops(True)
sage: G.allow_multiple_edges(True)

Now we are ready to add our edges by specifying a tuple of vertices that are connected by an edge. If there are multiple edges, we need to add the tuple with multiplicity.:

sage: G.add_edges([(0,0),(0,0),(0,1),(0,3),(1,3),(1,3)])

Now let us look at the graph!

sage: G.plot()
Graphics object consisting of 11 graphics primitives

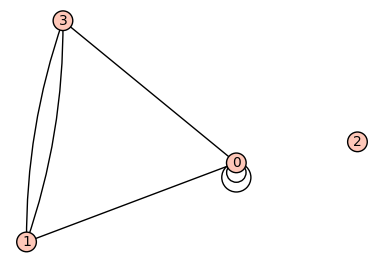
We can construct the adjacency matrix:

sage: A = G.adjacency_matrix()
sage: A
[2 1 0 1]
[1 0 0 2]
[0 0 0 0]
[1 2 0 0]

The entry in row $i$ and column $j$ of the $\ell$-th power of $A$ gives us the number of paths of length $\ell$ from vertex $i$ to vertex $j$. Let us verify this:

sage: A**2
[6 4 0 4]
[4 5 0 1]
[0 0 0 0]
[4 1 0 5]

There are 4 paths of length 2 from vertex $0$ to vertex $1$: take either loop at $0$ and then the edge $(0, 1)$ (2 choices) or take the edge $(0, 3)$ and then either of the two edges $(3, 1)$ (two choices):

sage: (A**2)[0,1]
4

To count the number of closed walks, we can also look at the sum of the $\ell$-th powers of the eigenvalues. Even though the eigenvalues are not integers, we find that the sum of their squares is an integer:

sage: A.eigenvalues()
[0, -2, 0.5857864376269049?, 3.414213562373095?]
sage: sum(la**2 for la in A.eigenvalues())
16.00000000000000?

We can achieve the same by looking at the trace of the $\ell$-th power of the matrix:

sage: (A**2).trace()
16